Category Archives: Science
 I hadn’t really planned to, but it’s both Pi Day and the birthday of Albert Einstein. As a fan of both the number and the man, it seems I should post something.
I hadn’t really planned to, but it’s both Pi Day and the birthday of Albert Einstein. As a fan of both the number and the man, it seems I should post something.
But I’ve written a lot about pi and Einstein, so — especially not having planned anything — I don’t have anything to say about either right now. In any event, I’m more inclined to celebrate Tau Day when we have double the pi(e). I do have something that’s maybe kind of vaguely of pi-ish. It’s something I was going to mention when I wrote about Well World.
It’s a little thing about hexagons.
Continue reading
2 Comments | tags: Albert Einstein, hexagon, pi day | posted in Math
 In the Rational vs Real post I mentioned that real numbers were each “an infinitely tiny island separated from direct contact with all other numbers.” The metaphor of each real number as an island comes from how, given any real number, it’s not possible to name the next (or previous) real number.
In the Rational vs Real post I mentioned that real numbers were each “an infinitely tiny island separated from direct contact with all other numbers.” The metaphor of each real number as an island comes from how, given any real number, it’s not possible to name the next (or previous) real number.
It’s easy enough to name a particular real number. For instance 1.0 and 3.14159… real numbers. There are infinitely many more we can name, but given any one of them, there is no way to get to any other number other than by explicitly naming it, too.
This applies to a variety of numeric spaces.
Continue reading
9 Comments | tags: complex numbers, continuum, integers, math theory, mathematics, natural numbers, numbers, rational numbers, real numbers, Theory of Mathematics | posted in Math
 One of the great philosophical conundrums involves the origin of numbers and mathematics. I first learned of it as Platonic vs Aristotelian views, but these days it’s generally called Platonism vs Nominalism. I usually think of it as the question of whether numbers are invented or discovered.
One of the great philosophical conundrums involves the origin of numbers and mathematics. I first learned of it as Platonic vs Aristotelian views, but these days it’s generally called Platonism vs Nominalism. I usually think of it as the question of whether numbers are invented or discovered.
Whatever it’s called, there is something transcendental about numbers and math. It’s hard not to discover (or invent) the natural numbers. Even from a theory standpoint, the natural numbers are very simply defined. Yet they directly invoke infinity — which doesn’t exist in the physical world.
There is also the “unreasonable effectiveness” of numbers in describing our world.
Continue reading
8 Comments | tags: math theory, mathematics, natural numbers, nominalism, numbers, Plato, Platonic, Platonism, rational numbers, real numbers, Theory of Mathematics | posted in Math, Philosophy
 I cracked up when I saw the headline: Why your brain is not a computer. I kept on grinning while reading it because it makes some of the same points I’ve tried to make here. It’s nice to know other people see these things, too; it’s not just me.
I cracked up when I saw the headline: Why your brain is not a computer. I kept on grinning while reading it because it makes some of the same points I’ve tried to make here. It’s nice to know other people see these things, too; it’s not just me.
Because, to quote an old gag line, “If you can keep your head when all about you are losing theirs… perhaps you’ve misunderstood the situation.” The prevailing attitude seems to be that brains are just machines that we’ll figure out, no big deal. So, it’s certainly (and ever) possible my skepticism represents my misunderstanding of the situation.
But if so, I’m apparently not the only one…
Continue reading
41 Comments | tags: algorithm, brain, brain mind problem, computationalism, consciousness, human brain, human consciousness, human mind, Matthew Cobb, mind, Theory of Consciousness | posted in Philosophy, Science
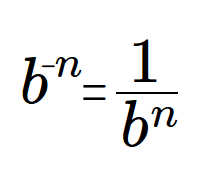 The last Sideband discussed two algorithms for producing digit strings in any number base (or radix) for integer and fractional numeric values. There are some minor points I didn’t have room to explore in that post, hence this follow-up post. I’ll warn you now: I am going to get down in the mathematical weeds a bit.
The last Sideband discussed two algorithms for producing digit strings in any number base (or radix) for integer and fractional numeric values. There are some minor points I didn’t have room to explore in that post, hence this follow-up post. I’ll warn you now: I am going to get down in the mathematical weeds a bit.
If you had any interest in expressing numbers in different bases, or wondered how other bases do fractions, the first post covered that. This post discusses some details I want to document.
The big one concerns numeric precision and accuracy.
Continue reading
3 Comments | tags: base 10, base 2, binary, binary digits, decimal, fractions, number bases | posted in Math, Sideband
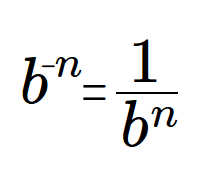
Fractional base basis.
I suspect very few people care about expressing fractional digits in any base other than good old base ten. Truthfully, it’s likely not that many people care about expressing factional digits in good old base ten. But if you’re in the tiny handful of those with an interest in such things — and don’t already know all about it — read on.
Recently I needed to figure out how to express binary fractions of decimal numbers. For example, 3.14159 in binary. And I needed the real thing — true binary fractions — not a fake that uses integers and a virtual decimal point.
The funny thing is: I think I’ve done this before.
Continue reading
4 Comments | tags: base 10, base 2, binary, binary digits, decimal, fractions, number bases | posted in Math, Sideband
 In this corner, philosopher John Searle (1932–), weighing in with what I like to call the Giant File Room (GFR). The essential idea is of a vast database capable of answering any question. The question it poses is whether we see this ability as “consciousness” behavior. (Searle’s implication is that we would not.)
In this corner, philosopher John Searle (1932–), weighing in with what I like to call the Giant File Room (GFR). The essential idea is of a vast database capable of answering any question. The question it poses is whether we see this ability as “consciousness” behavior. (Searle’s implication is that we would not.)
In that corner, philosopher and mathematician Kurt Gödel (1906–1978), weighing in with his Incompleteness Theorems. The essential idea there is that no consistent (arithmetic) system can prove all possible truths about itself.
It’s possible that Gödel has a knockout punch for Searle…
Continue reading
24 Comments | tags: algorithm, Incompleteness Theorems, John Searle, Kurt Gödel, The Chinese Room | posted in Philosophy, Science
 As a result of lurking on various online discussions, I’ve been thinking about computationalism in the context of structure versus function. It’s another way to frame the Yin-Yang tension between a simulation of a system’s functionality and that system’s physical structure.
As a result of lurking on various online discussions, I’ve been thinking about computationalism in the context of structure versus function. It’s another way to frame the Yin-Yang tension between a simulation of a system’s functionality and that system’s physical structure.
In the end, I think it does boil down the two opposing propositions I discussed in my Real vs Simulated post: [1] An arbitrarily precise numerical simulation of a system’s function; [2] Simulated X isn’t Y.
It all depends on exactly what consciousness is. What can structure provide that could not be functionally simulated?
Continue reading
7 Comments | tags: Alan Turing, algorithm, computationalism, consciousness, human brain, human consciousness, human mind, John Searle, semantic vectors, Theory of Consciousness, Turing Test | posted in Science

Ye Olden Tools of Yore
I’ve been meaning to write an Abacus post for years. I used one in my first job, back in high school, and they’ve appealed to me ever since. Many years ago I learned there were people who had no idea how an abacus worked. Until then I hadn’t internalized that it wasn’t common knowledge (maybe a consequence of learning something at an early age).
Recently, browsing through old Scientific American issues before recycling them, I read about slide rules, another calculating tool I’ve used, although, in this case, mainly for fun. My dad gave me his old slide rule from when he considered, and briefly pursued, being an architect.
So killing two birds with one stone…
Continue reading
28 Comments | tags: abacus, slide rule | posted in Life, Math

Complete Chaos!
One of my favorite discoveries in life is the Mandelbrot set. Considering it gives me a strong sense of the numinous. I’ve been enthralled by it ever since Fractint, an MS-DOS program that generated fractals. I’ve posted about it a lot here; today I want to take you into the heart of its chaotic behavior.
The Mandelbrot set has a number of properties that make it such a fascinating study: Firstly, it demonstrates chaos theory. Secondly, it demonstrates how complex patterns can arise from simple beginnings. Thirdly, it reveals a problem concerning real numbers. Fourthly, every pixel is a demonstration of Turing’s Halting Problem. It’s also infinitely complex and incredibly beautiful.
Today we’re going to explore the shore of the Mandelbrot lake.
Continue reading
7 Comments | tags: chaos, chaos theory, fractals, Mandelbrot, Mandelbrot fractal | posted in Science
 I hadn’t really planned to, but it’s both Pi Day and the birthday of Albert Einstein. As a fan of both the number and the man, it seems I should post something.
I hadn’t really planned to, but it’s both Pi Day and the birthday of Albert Einstein. As a fan of both the number and the man, it seems I should post something.
 One of the great philosophical conundrums involves the origin of numbers and mathematics. I first learned of it as Platonic vs
One of the great philosophical conundrums involves the origin of numbers and mathematics. I first learned of it as Platonic vs  I cracked up when I saw the headline:
I cracked up when I saw the headline: 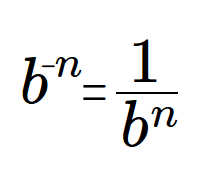
 In this corner, philosopher
In this corner, philosopher 













