 I’ve always liked (philosopher and cognitive scientist) David Chalmers. Of those working on a Theory of Mind, I often find myself aligned with how he sees things. Even when I don’t, I still find his views rational and well-constructed. I also like how he conditions his views and acknowledges controversy without disdain. A guy I’d love to have a beer with!
I’ve always liked (philosopher and cognitive scientist) David Chalmers. Of those working on a Theory of Mind, I often find myself aligned with how he sees things. Even when I don’t, I still find his views rational and well-constructed. I also like how he conditions his views and acknowledges controversy without disdain. A guy I’d love to have a beer with!
Back during the May Mind Marathon, I followed someone’s link to a paper Chalmers wrote. I looked at it briefly, found it interesting, and shelved it for later. Recently it popped up again on my friend Mike’s blog, plus my name was mentioned in connection with it, so I took a closer look and thought about it…
Then I thought about it some more…
The end result of all that thought is that I think Chalmers makes a misstep. Or, at least, what seems to me an unwarranted assumption.
It’s going to take some explaining. First, you should read A Computational Foundation for the Study of Cognition, by David Chalmers. I’ll be going through it in detail.
FWIW, one reason I like Chalmers is that he’s “skeptical about whether phenomenal properties can be explained in wholly physical terms.” [Footnote 4]
Or, at least in terms of yet undiscovered principles, but, yes, perhaps somehow transcending physics or what physics can analyze. (He is, after all, the guy who named The Hard Problem.)
§ §
In the Abstract, Chalmers writes: “Justifying the role of computation requires analysis of implementation, the nexus between abstract computations and concrete physical systems.”
I agree, so one thing I plan to do here is use some specificity regarding an implementation of the system Chalmers outlines.
Chalmers uses the terms “casual topology” and “organizational invariance” for key ideas I want to explore. He also defines a CSA (Combinatorial-State Automata, in contrast with an FSA or Finite-State Automata), which is especially important as a formalization of what he means by casual topology.
These all factor into what I think is missed, so I’ll go over my understanding of them in detail.
[This got long; I removed my word limit. (But no footnotes!)]
§
The notion of a CSA is central, so I’ll start there.
I need to presume you (the reader) have some grasp of an FSA (or FSM). [If not, see: Turing’s Machine or these … three … posts.]
The short form is: a system can be in a variety of states, and the behavior of that system can be specified in terms of transitions from state to state.
A CSA extends the idea such that inputs, outputs, and states, have multiple components. (Because typically, an FSA is viewed as dealing with single inputs, outputs, and states, although this isn’t a requirement.)
As Chalmers writes, “Finite CSAs, at least, are no more computationally powerful than FSAs; there is a natural correspondence that associates every finite CSA with an FSA with the same input/output behavior.” [section 2.1]
Indeed, and sometimes it’s a matter of interpretation.
For example, a simple FSA that validates the format of email addresses can be seen as taking (single) characters as inputs and having states labeled with (single) numbers.
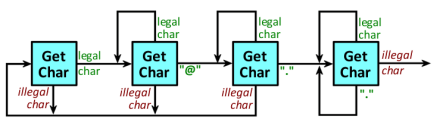
But look closer and see those input characters as vectors of bits. Those state labels, likewise, are vectors of bits. So the simple FSA can be seen as a CSA.
The reason for combinatorial complexity in design, as Chalmers writes, is: “First, […] a CSA description can therefore capture the causal organization of a system to a much finer grain. Second, the structure in CSA states can be of great explanatory utility.”
Exactly. The email validator makes more sense processing those vectors of bits as whole inputs and states. A bit-level implementation would be more complex and harder to understand (but certainly possible).
I agree with everything in the paper through the explanation of the CSA and into section 2.2. I would like to return to the last four questions in that section (digestion, Putnam, semantics, computers). Not that I disagree (I don’t). It’s more that I have some comments.
In fact, it’s not until section 3.3 that I think there’s a problem. I’ll get to that, but first I want to consider organizational invariance and causal topology.
§ §
Chalmers introduces both terms in section 3.1. Of the latter he writes:
The causal topology represents the abstract causal organization of the system: that is, the pattern of interaction among parts of the system, abstracted away from the make-up of individual parts and from the way the causal connections are implemented.
And later, in section 3.3:
In fact, it turns out that the CSA formalism provides a perfect formalization of the notion of causal topology. A CSA description specifies a division of a system into parts, a space of states for each part, and a pattern of interaction between these states. This is precisely what is constitutive of causal topology.
[Emphasis mine in both quotes.]
So the causal topology of a system is an abstraction (a formalism) — it is crucial to fully appreciate what that means in the context of what Chalmers wrote to start: “…implementation, the nexus between abstract computations and concrete physical systems.”
I couldn’t agree more. It means we need to talk seriously about what actually happens in any putative implementation (including the brain itself).
§
Before we get to that, the other term, organizational invariance, is about system properties that remain constant so long causal topology is preserved.
I wonder if this notion isn’t a little loose. Chalmers writes that a tube of toothpaste isn’t invariant because replacing the toothpaste with peanut butter means it’s not a tube of toothpaste anymore.
Fine, but why doesn’t replacing a mind with computation (let alone brain parts with silicon) mean it’s not a mind anymore? Those seem more extreme changes to me.
In section 3.2, Chalmers writes: “The central claim of this section is that most mental properties are organizational invariants.”
This seems to need a post of its own to explore exactly how organizational invariance relates to mental properties. I don’t see it as affecting the main point, so I’ll accept it provisionally.
I think what is important is the latter part of section 3.2, the “dancing qualia” thought scenario.
[See Absent Qualia, Fading Qualia, Dancing Qualia, by David Chalmers, for more about organizational invariance and qualia scenarios.]
§
Here’s the thing: (To the extent such a substitution could be possible) I quite agree that (it seems likely) mental properties would be preserved.
I’ve always said a Positronic Brain ought to work and that I’d be more surprised if it didn’t work. The dancing qualia scenario is essentially replacing the brain with a Positronic Brain, so of course I think that should work.
In this case, I agree organization is invariant and causal topology is preserved. (The whole point is that this replacement preserves causal topology.)
Where things jump the shark is section 3.3 — the presumption that a numerical simulation is the same thing.
§ §
The presumption is that, if The Algorithm describing how states change is executed on an appropriate Engine with appropriate Data, this results in mental states of cognition.
The rationale is that causal topology is preserved by The Algorithm.
I think this is debatable (if not false).
(Note that Chalmers explicitly says his approach deals with cognition rather than phenomenology: “Alternatively, the version of the thesis most directly supported by the argument in the text is that computation provides a general framework for the mechanistic explanation of cognitive processes and behavior.” [Footnote 6])
§
In order to examine this, let’s put some specificity to the CSA Chalmers imagines will generate mental states.
Wikipedia puts the human brain at having 86 billion neurons. Let’s assume our numerical simulation gets by okay with just 50 billion.
The number of synapses varies from 100 to 1,000 trillion (the latter in the very young). That’s a fair range (an order of magnitude).
Wiki also says neurons have on average 7,000 synaptic connections. Let’s have our numerical model get by with just 5,000 synaptic connections per neuron (on average).
Then we have 5×1010 neurons times 5×103 connections giving us 2.5×1014 synapses. That’s 250 trillion synapses.
This matters with regard to the implementation of the Mind CSA.
Chalmers writes: “The fine-grained causal topology of a brain can be specified as a CSA.”
One question here is whether the state vectors should be neuron states or synapse states — I think there’s a strong argument to grain this at the synapse level. That means each CSA state vector has 250 trillion components. (Alternatively, at the neuron level, each state vector has 50 billion components.)
Multiply those numbers by however many bits it takes to represent a state (say, 64) to obtain the final size requirement.
§ §
Let’s also specify the computational system. It consists of four basic parts:
- The “register” holding the current system state, S.
- The model, M, that describes the (brain) system.
- The program, P, that encodes the system’s causality.
- The engine, E, that executes P (using M to modify S).
As an aside, note that S is large (either 50 giga or 250 tera). M is even larger. [See: The Human Connectome]
It’s likely that P is fairly large, too, considering what it has to do. E is essentially any modern CPU, so weighs in somewhere in the multi-terabyte range.
(P and E have a high degree of complexity; S and M are structurally very simple; they’re just lists of numbers.)
§
What all this does is calculate the next state of the system. Let’s take a close look at what that involves.
The engine, E, repeatedly fetches bit patterns from P, and interprets each pattern as a valid instruction it knows how to perform. Such instructions fall into one of five classes: fetch data, store data, modify data, test data, transfer control (i.e. jumps and calls).
In order to perform these tasks, most engines are self-contained computers in their own right. They operate according to an algorithm.
As a consequence of executing lots of instructions in sequence, the algorithm encoded in P is executed to create the next state, S (remember that S is very large, so lots of changes are required).
Some components of S can be taken as inputs and some as outputs. As such, the next state for S completely depends on the current state, and output is generated in consequence of the changing states of S.
§
Now I want to focus on S and its “register” — and also on P (which encodes the causal topology of the physical system being simulated).
There are many ways to implement a memory register. Modern computers usually use a capacitor-based circuit or a transistor-based flip-flop circuit, but the details don’t matter. For specificity, we’ll pick the capacitors.
This means the register for S has, low-end, 3.2 trillion capacitors (16 quadrillion, high-end), assuming 64-bits per component.
The key point is that each capacitor, each bit, stands alone.
They are connected to power and control lines, but none of them are connected to each other. None of them have any causal connection with each other.
What’s more, there is no causality behind what state they have, or which state they have next. There is no connection between states or between bits — both are fully independent.
Compare this to the state of a neuron, where the next state very much depends on the current state and directly on the state of input neurons.
§
At a higher level, groups of 64 capacitors comprise a 64-bit number, which is interpreted as representing the state of a neuron or synapse.
I can’t stress enough the disconnect between the actual physical brain state and the 64-digit binary number (represented by 64 capacitors) that has been assigned to stand for that state.
Physical neurons have a physical state, not a number. Physicality, not information.
§
It seems clear the answer can’t lie in the states themselves. They have no causal topology on their own.
The causal topology we need must lie in program P (with reference to engine E).
The physical computer has a clear causal topology that enables it to be a computer. This involves currents, voltages, transistors, and other electronic components.
The physical causality of the computer compares to our physical causality. In both cases that physicality defines.
At a higher level, parts of the computer have different casual topology. As mentioned, the engine E is a stand-alone computer (somewhat comparable, perhaps, to sub-systems of the brain).
The entire working system (P, E, S, M) has a causal topology, and it is this level of causality claimed to create mental states. (Or, at least, predict behavior.)
§
I have two objections to this. The first involves all those underlying layers of causality — layers that are significantly different from the causality they implement.
In the brain, the lowest layers of the implementation directly reflect the casual topology. Flows through neurons reflect actual signals caused by inputs, which directly cause synapses to react.
My other objection is that, computationally, the causality being implemented is the abstraction, the description of the thing, rather than the thing.
Consider pulling a cord attached to a bell so the bell rings. On the other hand, consider writing a code on paper and handing that to someone who interprets that code as instructions to ring the bell.
Either way the bell rings, but the former process is physical, direct, and immediate, while the latter is informational, indirect, and delayed.
Either way the bell rings, but to the extent process matters, the processes are entirely different. Put another way, the causal chains involved are completely different.
§
It boils down to how much process matters. It boils down to whether the divide between physicality and information matters.
I see enough differences to be skeptical, others find them unimportant.
The creation of mental states can’t lie in the separate capacitors nor in the numbers they form. If anything, it has to lie in the instruction fetch-decode-execute cycles of the CPU operating over the bit patterns of program P.
But given the closed instruction set of the engine, given it’s just bits and logical operations, it’s hard to see how that can really invoke the necessary causal topology.
At best it remains highly abstract, and I’m not sure that counts.
§
This has gotten long, and there’s quite a bit more to talk about. I don’t see an obvious place to break this in two, but I have reached an obvious stopping point.
Until next time!
Stay topologically casual, my friends!
∇













June 21st, 2019 at 7:58 pm
It occurred to me that something which might not be apparent to those who have debated computationalism with me is that I came to be skeptical of it through reading, discussing, and writing, about it.
As someone who got into computer science and software design back in the late 1970s, and as someone who has read science fiction since childhood, I always just assumed computers would “think” (kinda like everyone did back then — it was just assumed AI would work out eventually).
It’s only through really getting into it, reading various papers, and through working ideas out in debate, that I’ve come to see computationalism as potentially problematic (on multiple grounds).
So my opinion on this is really not a matter of intuitive bias. If anything, the bias was the other way. It’s rational thought that made me this way!
June 22nd, 2019 at 12:26 am
That mental states cannot possibly be found in the reification of computed states (that is, the register for S) is obvious in that the numbers (bit patterns) representing them could be anything. The numbers are just representational symbols mapped to physical states. Since those numbers could have any values — the values have no intrinsic meaning — they can’t have mental content.
Of course, the contention is that meaning exists in The Algorithm, which I’ll explore in future posts.
The point of interest here is that the computational states having no meaning is quite different from the physical situation in the brain where the brain states are the meaning.
Put it this way: We can change the numbers used to represent states in the computation without affecting the computation at all. We can’t equally change brain states to different values without affecting mental content.
June 22nd, 2019 at 2:24 pm
I think the capacitors / transistors ,etc, remain part of the causal topology. But I can see your point that the topology is very different. Chalmers’ conception can be sustained by abstracting away the lower level parts of it, but that’s admittedly abstracting away part of the computation, a consequence of emulating one information processing architecture on another. And it’s based on an understanding of cognition being information processing. If you’re convinced it’s not that, or more than that, then I can see your concern.
And, as I’ve noted before, I also think the differences can make a big difference in performance, power consumption, etc, meaning massive physical parallelism might be mandatory strictly as a pragmatic matter. I don’t know if we need to go all the way to a positronic brain (whatever that means) but the petering out of Moore’s Law probably means trying to do it with serial processing may never be practical.
On pulling a cord attached to a bell, I think the relevant aspect is that the pull powers the bell, which doesn’t have its own energy source. Sending a message to someone to do it doesn’t have that aspect. But in both technological computers and nervous systems, the signal doesn’t power what happens next. In both systems, the next component in the causal chain (generally) has its own energy source.
June 22nd, 2019 at 3:58 pm
“I think the capacitors / transistors ,etc, remain part of the causal topology.”
Ha! Funny you say that. I just finished the first draft of the continuation post, and said much the same thing. At the least, they’re the memory the system uses to determine the next state.
It raises an interesting question, then. What happens if we record the states and then just play them back into the register one after the other? The memory would go through the exact same set of states, but no algorithm (or at least a radically different one) is driving those changes.
Does that result in cognition? If it does, it argues the algorithm doesn’t matter. If it doesn’t, then what do the states really mean?
I wonder if it all doesn’t end up being an argument that physical causal topology is not preserved in algorithms. (Neo certainly defied it in the Matrix. 🙂 )
“Chalmers’ conception can be sustained by abstracting away the lower level parts of it…”
I don’t think that’s right. Chalmers explicitly talks about the need for the algorithmic system to have the necessary fine grain. His whole point requires demonstrating that both systems, in some sense, have the same causal topology. The more the systems are treated as blackboxes, the harder that case is to make.
(And my point is I’m not sure the jump from physical reality to numerical simulations preserves causal topology in any meaningful way.)
“I also think the differences can make a big difference in performance, power consumption, etc,”
Hugely! And some kinds of algorithms are less efficient than others. State engines tend to be among the less, although they have their advantages. The bigger issue is that such algorithms tend to have large data requirements. On top of the vast sizes needed to deal with cognition in the first place. Compounds the size problem, I’m saying.
“On pulling a cord attached to a bell, I think the relevant aspect is that the pull powers the bell, which doesn’t have its own energy source.”
I know what you mean (though one can argue that large bells are powered a lot by their own mass and weight. Church bells are rolled into horizontal position and then let fall — it’s the falling of the bell against the clapper that rings it).
It’s a good way to distinguish a signal (which I think additionally requires a physical causal chain) from not signal. I think in this case the focal point is the actual physical chain of causality versus the abstract implicit causality implied by executing an algorithm.
Chalmers’ claim is that the executed algorithm preserves it. I’m not sure.
June 22nd, 2019 at 5:59 pm
“His whole point requires demonstrating that both systems, in some sense, have the same causal topology.”
I do think that’s achievable, but in the technology at a higher level than the hardware architecture.
“And my point is I’m not sure the jump from physical reality to numerical simulations preserves causal topology in any meaningful way.”
But in the implementation, I don’t think that jump ever actually happens. Remember, the implementation is always a 100% physical system, and can be modeled purely at that level. Which means the information flows, even in, say, a software ANN running in a virtual machine, are ultimately physical events.
But as I conceded above, it’s embedded in the broader physical system of the computer. For me, as someone convinced it’s all information processing anyway, it doesn’t matter (except possibly in practical terms of capacity and performance). But if you’re convinced that there’s more there (like hurricane-ness or tooth-paste-ness), then it does.
“versus the abstract implicit causality implied by executing an algorithm.”
But how is that not itself physical? Isn’t any instantiation of software physical? The physicality may be scattered within a broader physical system, but it seems to me like it’s still definitely there.
And it’s worth noting that the causal topology from the biology is itself scattered within a physical system (involving genes, glial cells, etc). The only question, it seems to me, is which parts of that physical system are necessary to reproduce the system’s broader causal effects.
June 22nd, 2019 at 7:27 pm
“I do think that’s achievable, but in the technology at a higher level than the hardware architecture.”
I’m not sure it’s truly found at any technological level (if technology equals hardware). The problem I’m seeing is that, it is there, but only at the abstract level.
I said in today’s post, it kind of exists only in the programmer’s head.
This is evident in that any program only produces lists of numbers. It’s up to the programmer to apply those meaningfully. The map of numbers to real-world results is due to the programmer (as is the entire map of the program).
As an example, when I write code that models a chess game, I design an abstract data structure that represents the board, pieces, and moves. And how the program’s outputs (the lists of numbers) are applied usefully (as a print out, display, or whatever).
[I went on to write more about this, but then realized it would be worth posting on my programming blog (for reasons you’ll understand once you see it). I’ll let you know when that post is up.]
“Remember, the implementation is always a 100% physical system,”
Yes, but part of the point is that the physical causality of the implementation is nothing at all like the physical causality being simulated in the abstraction.
In the brain, the physical causality maps directly to the process the physical brain performs. The two are the same thing.
In a computer, the physical causality is only that of a computer performing physical computer operations. Those operations have no relationship to the abstract causality they model. (They can do any computation.)
“For me, as someone convinced it’s all information processing anyway,”
Unless one takes the Tegmarkian view, I think that concession is crucial.
The output numbers of a bridge simulation tells us whether the real bridge will carry weight. The output numbers of an airplane simulation tell us whether the real airplane will fly.
But we don’t expect the simulation to carry weight or fly.
Why do computationalists view a simulation of the brain so differently? They expect it to be a brain.
As you say, the only answer is the informational view, that’s the only way that works. That’s the only way a simulation can be the thing it simulates.
Which means you may have to concede the brain is special, after all, since nothing else physical is information-based like that. With no other physical system do we expect the simulation to be the thing. 🙂
“Isn’t any instantiation of software physical?”
Yes, but that physicality is completely unrelated to the physicality of the system it’s modeling. As we often point out, software (computation) is platform-agnostic. (Brains, obviously, are not. They are the platform.)
Two physical systems, yes, but in one the causal topology of the process is low-level, physical, and direct, while in the other the causal topology of the process is, at best, high-level, abstract, and indirect.
Or possibly not really existing at all, except in the mind of the programmer. (Pretty much as in all video games that simulate some sort of reality.)
“The only question, it seems to me, is which parts of that physical system are necessary to reproduce the system’s broader causal effects.”
In the context of this paper, Chalmers might disagree. (??) He seems to feel the simulation needs to be fairly fine-grained. He posits neuron-level, although he also says perhaps something higher might work (without mention how high he has in mind).
This is, perhaps, where you go further than Chalmers in accepting high-level behavior regardless of the mechanism achieving it. Or such is my impression (that he, as I am, is interested more in the mechanism, the why and how).
June 23rd, 2019 at 9:51 am
“Which means you may have to concede the brain is special, after all, since nothing else physical is information-based like that.”
Nervous systems and computers 🙂 Oh, and possibly the processing between the sensorium and motorium of some unicellular organisms, although those seem more borderline.
“This is, perhaps, where you go further than Chalmers in accepting high-level behavior regardless of the mechanism achieving it.”
In terms of cognition, I think I’m mostly in alignment with Chalmers. Although I suspect there are functional alternatives I’m open to that he might object to, maybe.
Where there is a difference between us is in our attitude toward phenomenal properties. He’s not convinced they’re physical, although he sees them as dependent on physical properties, organizational properties in particular. This seems like dualism (he does label himself a naturalistic dualist) but a dualism channeled through computation.
My view is simpler. Phenomenal properties are information.
June 23rd, 2019 at 11:31 am
“Nervous systems and computers”
The nervous systems in the brain, yes, that is what is presumed to be an information system capable of being simulated successfully. (The whole question is whether that’s true.)
Computers (computation), yes also, but of course I was speaking of natural physical systems. (The physical computers, as I mentioned with calculators, cannot be successfully simulated in that shorting out the power supply does no damage. Nor does such a system generate heat or emit photons.)
We can go around on this forever. You don’t see much difference between information systems and physical systems. I admit I totally don’t understand that, they’re Yin and Yang to me, but I’m tired of trying to convince you otherwise. I give up.
“Where there is a difference between us is in our attitude toward phenomenal properties.”
Yeah, that’s what I was thinking. Obviously I tend to align with his view.
“My view is simpler.”
Ha! I can quote back that supposed Einstein phrase you once quoted to me (for reasons I can’t remember): “Everything should be made as simple as possible, but not simpler.”
A great maxim (sometimes called “Einstein’s Razor”), but he never wrote anything exactly like it. He apparently said something roughly similar in a lecture, and he did write, “It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.”
(Which so sounds like him! 🙂 )
Poor Al,… he’s the most misquoted guy on the planet!
Which is to say that such an informational view might turn out to be overly simple. Or not. Maybe Tegmark is right!
It certainly explains why you don’t see much divide between physical systems and information systems — you classify them both as the latter.
June 23rd, 2019 at 3:50 pm
FWIW: The Eight Queens.
It’s an example of an abstract problem that’s usually thought of as being reified in some physical system. (The Traveling Salesman is another example, but much harder to solve. 🙂 )
As such, the first approximation is to model the physicality (as I show in the first three versions). Thinking about it more deeply can result in a more elegant approach based on the mathematics (the actual abstraction).
In contrast, when modeling the full-adder, the usual route is to model the abstraction (which, in this case, is far simpler than any physical model). Physical models there were quite involved.
I thought The Eight Queens was an interesting example of just how abstract notions of causality are in software. The problem is based on an arbitrary rule not reflected in physical reality — there’s nothing wrong with placing queens on a chessboard such that one can immediately capture another.
It’s not smart, but it’s not forbidden. 😀
I thought, too, it was an interesting example of how abstract the data structures used in a model can be. The “board” behind the first three versions is really a row list of column lists — a data structure with no relation to an 8×8 grid.
Even an array is actually a contiguous group of locations, the two dimensional nature is an abstraction.
The fourth example doesn’t really model reality at all. There is no board, there are no queens.
Yet the code displays both types of models the same way. The bit of printout shown is generated by all four versions.
OTOH, given your informational view, it would all fall under the same heading for you, so probably not that interesting after all.
July 2nd, 2024 at 3:16 pm
[…] Combinatorial-State Automata (CSA). I’m trying to better express ideas I first wrote about in these three […]
July 2nd, 2024 at 3:22 pm
[…] month I wrote three posts about a proposition by philosopher and cognitive scientist David Chalmers — the idea […]