Category Archives: Science
The word “always” always finds itself in phrases such as “I’ve always loved Star Trek!” I’ve always wondered about that — it’s rarely literally true. (I suppose it could be “literally” true, though. Language is odd, not even.) The implied sense, obviously, is “as long as I could have.”
The last years or so I’ve always been trying to instead say, “I’ve long loved Star Trek!” (although, bad example, I don’t anymore; 50 years was enough). Still, it remains true I loved Star Trek for a long (long) time.
On the other hand, it is literally true that I’ve always loved science.
Continue reading
12 Comments | tags: MIT OCW, QM101, quantum computing, quantum mechanics, Scientific American | posted in Physics
A crushed flower.
This post has nothing to do with Amy Winehouse, sadly on the list of great talents who, poorly served by those in their lives, lost their way and died tragically and long before their time. (It’s bad enough when the ravages of life — disease and accident — steal away those with gifts. Losing people to human foibles is a more painful loss.)
The topic here is the Block Universe Hypothesis, which I’m revisiting, so the title kinda grabbed me (and I am a Winehouse fan). I’ve written about the BUH before, but a second debate with the same opponent turned up a few points worth exploring.
So it’s back to basic block (everyone looks good in block?)…
Continue reading
31 Comments | tags: block universe, simultaneity, Special Relativity | posted in Physics
Among those who study the human mind and consciousness, there is what is termed “The Hard Problem.” It is in contrast to, and qualitatively different from, problems that are merely hard. (Simply put, The Hard Problem is the question of how subjective experience arises from the physical mechanism of the brain.)
This post isn’t about that at all. It’s not even about the human mind (or about politics). This post is about good old fundamental physics. That is to say, basic reality. Some time ago, a friend asked me what was missing from our picture of physics. This is, in part, my answer.
There is quite a bit, as it turns out, and it’s something I like to remind myself of from time to time, so I made a list.
Continue reading
26 Comments | tags: big bang, block universe, cosmology, dark energy, dark matter, Many Worlds Interpretation, Mathematical Universe Hypothesis, MUH, MWI, quantum physics, standard model, universe, virtual reality | posted in Physics
I just finished reading Beyond Weird: Why Everything You Thought You Knew About Quantum Physics Is Different (2018) by science writer Philip Ball. I like Ball a lot. He seems well grounded in physical reality, and I find his writing style generally transparent, clear, and precise.
As is often the case with physics books like these, the last chapter or three can get a bit speculative, even a bit vague, as the author looks forward to imagined future discoveries or, groundwork completed, now presents their own view. Which is fine with me so long as it’s well bracketed as speculation. I give Ball high marks all around.
The theme of the book is what Ball means by “beyond weird.”
Continue reading
12 Comments | tags: Philip Ball, quantum mechanics, wave-function | posted in Books, Physics
Since I retired, I’ve been learning and exploring the mathematics and details of quantum mechanics. There is a point with quantum theory where language and intuition fail, and only the math expresses our understanding. The irony of quantum theory is that no one understands what the math means (but it works really well).
Recently I’ve felt comfortable enough with the math to start exploring a more challenging aspect of the mechanics: quantum computing. As with quantum anything, part of the challenge involves “impossible” ideas.
Like the square root of NOT.
Continue reading
21 Comments | tags: Artur Ekert, Philip Ball, quantum computing | posted in Computers, Physics
With COVID-19 putting a damper on social activity, “the gang” doesn’t get together very often, but we still gather occasionally (and carefully). One of the times recently I got into how, even though we’re all sitting essentially motionless in a living room, we’re moving through time at the speed of light. I explained why that was, and they found it pretty cool.
Then I ran into someone online who just couldn’t wrap his head around it — just couldn’t accept it (despite explaining in detail and even providing links to some videos). Physics is sometimes challenging to our daily perceptions of reality!
In this case, though, it’s just a matter of some rather simple geometry.
Continue reading
17 Comments | tags: frame of reference, light speed, Lorentz equation, spacetime, Special Relativity, velocity | posted in Physics
Converging…
Back in October I published two posts involving the ubiquitous exponential function. [see: Circular Math and Fourier Geometry] The posts were primarily about Fourier transforms, but the exponential function is a key aspect of how they work.
We write it as ex or as exp(x) — those are equivalent forms. The latter has a formal definition that allows for the complex numbers necessary in physics. That definition is of a series that converges on an answer of increasing accuracy.
As a sidebar, I thought I’d illustrate that convergence. There’s an interesting non-linear aspect to it.
Continue reading
9 Comments | tags: exponential function, transcendental numbers | posted in Math, Sideband
And the total is…?
Oh the irony of it all. Two days ago I post about two math books, at least one of which (if not both) I think everyone should read. This morning, reading my newsfeed, I see one of those “People Are Confused By This Math Problem” articles that pop up from time to time.
Often those are expressions without parentheses, so they require knowledge of operator precedence. (I think such “problems” are dumb. Precedence isn’t set in stone; always use parentheses.)
Some math problems do have a legitimately confusing aspect, but my mind is bit blown that anyone gets this one wrong.
Continue reading
10 Comments | tags: fun with numbers, math phobia, mathematics | posted in Math, Rant, Society
There are many science-minded authors and working physicists who write popular science books. While there aren’t as many math-minded authors or working mathematicians writing popular math books, it’s not a null set. I’ve explored two such authors recently: mathematician Steven Strogatz and author David Berlinski.
Strogatz wrote The Joy of X (2012), which was based on his New York Times columns popularizing mathematics. I would call that a must-read for anyone with a general interest in mathematics. I just finished his most recent, Infinite Powers (2019), and liked it even more.
Berlinski, on the other hand, I wouldn’t grant space on my bookshelf.
Continue reading
11 Comments | tags: calculus, David Berlinski, derivatives, fun with numbers, integrals, numbers, Steven Strogatz, The Joy of X | posted in Books, Math
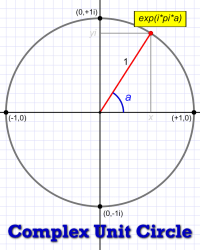Last time I opened with basic exponentiation and raised it to the idea of complex exponents (which may, or may not, have been surprising to you). I also began exploring the ubiquitous exp function, which enables the complex math needed to deal with such exponents.
The exp(x) function, which is the same as ex, appears widely throughout physics. The complex version, exp(ix), is especially common in wave-based physics (such as optics, sound, and quantum mechanics). It’s instrumental in the Fourier transform.
Which in turn is as instrumental to mathematicians and physicists as a hammer is to carpenters and pianos.
Continue reading
8 Comments | tags: complex numbers, complex plane, exponential function, exponentiation, Fourier transform, Heisenberg Uncertainty | posted in Math, Physics
Logos con carne 