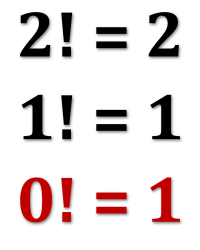Recently, I learned an interesting new math trick involving what are known as dual numbers. These are compound numbers similar in form to complex numbers but with a different kind of “magic” element enabling their behavior.
What makes them interesting to people like me is the surprising way they provide a fast and easy technique for software to generate the derivative of a given function.
As an unrelated bonus, a simple explanation of why zero-factorial is equal to one rather than zero (which might seem more intuitive).
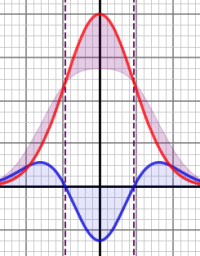This is the first of a series of posts exploring the mysterious Schrödinger Equation — a central player of quantum mechanics. 
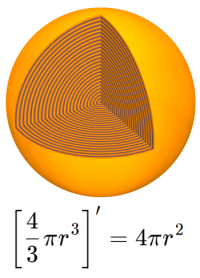I’ve always had a strong curiosity about how things work. My dad used to despair how I’d take things apart but rarely put them back together. My interest was inside — in understanding the mechanism. (The irony is that I began my corporate career arc as a hardware repair technician.)
Today is the first Earth-Solar event of 2021 — the 
There are many science-minded authors and working physicists who write popular science books. While there aren’t as many math-minded authors or working mathematicians writing popular math books, it’s not a null set. I’ve explored two such authors recently: mathematician 
Logos con carne 