Category Archives: Science
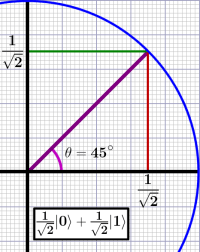 It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the Born Rule is really just another case of the Pythagorean theorem. The connection is in the way the coefficients of a quantum superposition, when squared, must sum to unity (one).
It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the Born Rule is really just another case of the Pythagorean theorem. The connection is in the way the coefficients of a quantum superposition, when squared, must sum to unity (one).
For that matter, Special Relativity, which is entirely geometric, is yet another example of the Pythagorean theorem, but that’s another story. (One I’ve already told. See: SR #X6: Moving at Light Speed)
The obvious connection is the geometry behind how a quantum state projects onto the basis eigenvectors axes.
Continue reading
9 Comments | tags: geometry, Pythagoras, QM101, quantum mechanics, trigonometry | posted in Brain Bubble, Math, Physics
 In The Road to Reality (2004), Roger Penrose writes about a great analogy for symmetry breaking. Apparently, this analogy is rather common in the literature. (No, it’s not the thing about the pencil — this one involves an iron ball.) Once again, I find myself agreeing with Penrose about something; it is a great analogy.
In The Road to Reality (2004), Roger Penrose writes about a great analogy for symmetry breaking. Apparently, this analogy is rather common in the literature. (No, it’s not the thing about the pencil — this one involves an iron ball.) Once again, I find myself agreeing with Penrose about something; it is a great analogy.
Symmetry breaking (which can be explicit or spontaneous) is critical in many areas of physics. For instance, it’s instrumental in the Higgs mechanism that’s responsible for the mass of some particles.
The short post is for those interested in physics who (like I) have struggled to understand exactly what symmetry breaking is and why it matters.
Continue reading
5 Comments | tags: QM101, Roger Penrose, symmetry | posted in Brain Bubble, Physics
 I started 2022 with a post titled Things I Think Are True. It was an echo of the Hard Problems post I’d done to start 2021. That earlier post listed a (possibly surprising) number of open questions in physics. Not trivial questions, either, but big ones like: “What is time?” and “What is the shape and size of the universe?”
I started 2022 with a post titled Things I Think Are True. It was an echo of the Hard Problems post I’d done to start 2021. That earlier post listed a (possibly surprising) number of open questions in physics. Not trivial questions, either, but big ones like: “What is time?” and “What is the shape and size of the universe?”
The post in 2022 was more of an opinion piece about things that, in the context of those open questions, I think are true. Pure speculation on my part, some of it close to mainstream thinking, some of it rather less so (but all, I would argue, grounded in what we do know).
This year, for contrast, I thought I’d make a list of stuff I don’t believe is true.
Continue reading
16 Comments | tags: causal determinism, computationalism, eternal inflation, ghosts, MWI, String theory, supersymmetry, time travel | posted in Opinion, Physics
 Last time I began exploring the similarity between the Schrödinger equation and a classical heat diffusion equation. In both cases, valid solutions push the high curvature parts of their respective functions towards flatness. The effect is generally an averaging out in whatever space the function occupies.
Last time I began exploring the similarity between the Schrödinger equation and a classical heat diffusion equation. In both cases, valid solutions push the high curvature parts of their respective functions towards flatness. The effect is generally an averaging out in whatever space the function occupies.
Both equations involve partial derivatives, and I ignored that in our simple one-dimensional case. Regular derivatives were sufficient. But math in two dimensions, let alone in three, requires partial derivatives.
Which were yet another hill I faced trying to understand physics math. If they are as opaque to you as they were to me, read on…
Continue reading
11 Comments | tags: derivatives, exponential function, partial derivatives, QM101, Schrödinger Equation | posted in Math, Physics
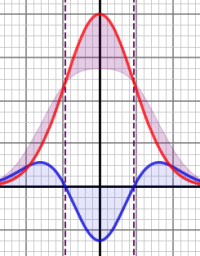 This is the first of a series of posts exploring the mysterious Schrödinger Equation — a central player of quantum mechanics. Previous QM-101 posts have covered important foundational topics. Now it’s time to begin exploring that infamous, and perhaps intimidating, equation.
This is the first of a series of posts exploring the mysterious Schrödinger Equation — a central player of quantum mechanics. Previous QM-101 posts have covered important foundational topics. Now it’s time to begin exploring that infamous, and perhaps intimidating, equation.
We’ll start with something similar, a classical equation that, among other things, governs how heat diffuses through a material. For simplicity, we’ll first consider a one-dimensional example — a thin metal rod. (Not truly one-dimensional, but reasonably close.)
Traveller’s Advisory: Math and graphs ahead!
Continue reading
9 Comments | tags: derivatives, exponential function, QM101, quantum, Schrödinger Equation | posted in Math, Physics

“Time is out of joint.”
I’ve long puzzled over the idea that physics is reversible. That its laws, with some caveats, work the same if time runs forwards or backwards. It’s even been suggested that, except for entropy, time could run backwards just as easily as forwards.
But this seems contrary to our everyday experience. With some exceptions, we can tell if a film or video clip is shown in reverse. Objects that fall, break, or grow (such as plants or crystals), look different seen in reverse.
I think there is more going on there than just entropy.
Continue reading
30 Comments | tags: arrow of time, time | posted in Physics
If you follow stuff like this, you probably already know, but the James Webb Space Telescope team just released the first actual image from the telescope:

More images are expected to be released tomorrow (July 12). Visit their page for details (and the full-sized image — all 4537×4630 pixels of it). Visit their excellent “Where Is Webb?” page for the latest status and stats on the JWST.
Congrats again to everyone involved! This was an amazing (and prolonged) effort. I’m glad I get to see some of the results now!
7 Comments | tags: astronomy, James Webb Space Telescope, JWST, space | posted in Science
 A single line from a blog post I read got me wondering if maybe (just maybe) the answer to a key quantum question has been figuratively lurking under our noses all along.
A single line from a blog post I read got me wondering if maybe (just maybe) the answer to a key quantum question has been figuratively lurking under our noses all along.
Put as simply as possible, the question is this: Why is the realm of the very tiny so different from the larger world? (There’s a cosmological question on the other end involving gravity and the realm of the very vast, but that’s another post.)
Here, the answer just might involve the wavelength of matter.
Continue reading
9 Comments | tags: de Broglie wavelength, QM101, quantum computing, quantum mechanics, qubits | posted in Opinion, Physics
 I’ve been working my way through The Principles of Quantum Mechanics (1930), by Paul Dirac. (It’s available as a Kindle eBook for only 6.49 USD.) It’s perhaps best known for being where he defines and describes his 〈bra|ket〉 notation (which I posted about in QM 101: Bra-Ket Notation). More significantly, Dirac shows how to build a mathematical quantum theory from the ground up.
I’ve been working my way through The Principles of Quantum Mechanics (1930), by Paul Dirac. (It’s available as a Kindle eBook for only 6.49 USD.) It’s perhaps best known for being where he defines and describes his 〈bra|ket〉 notation (which I posted about in QM 101: Bra-Ket Notation). More significantly, Dirac shows how to build a mathematical quantum theory from the ground up.
This is not a pop-science book. Common wisdom is that including even a single equation in a science book greatly reduces reader interest. Dirac’s book, in its 82 chapters, has 785 equations! (And no diagrams, which is a pity. I like diagrams.)
What I wanted to post about is something he mentioned about qubits.
Continue reading
14 Comments | tags: Bloch sphere, bra-ket notation, Paul Dirac, QM101, quantum computing, quantum mechanics, qubits | posted in Physics
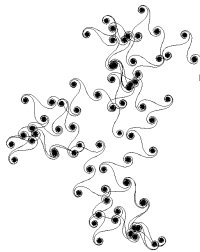 I posted a while back about the wonders of Fourier Curves, and I’ve posted many times about Euler’s Formula and other graphical wonders of the complex plane. Recently, a Numberphile video introduced me to another graphical wonder: Euler Spirals. They’re one of those very simple ideas that results in almost infinite variety (because of chaos).
I posted a while back about the wonders of Fourier Curves, and I’ve posted many times about Euler’s Formula and other graphical wonders of the complex plane. Recently, a Numberphile video introduced me to another graphical wonder: Euler Spirals. They’re one of those very simple ideas that results in almost infinite variety (because of chaos).
As it turned out, the video (videos, actually) led to a number of fun diversions that have kept me occupied recently. (Numberphile has inspired more than a few projects over the years. Cool ideas I just had to try for myself.)
This all has to do with virtual turtles.
Continue reading
10 Comments | tags: geometry, Leonhard Euler, Numberphile, pi | posted in Math, Wednesday Wow
 It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the Born Rule is really just another case of the Pythagorean theorem. The connection is in the way the coefficients of a quantum superposition, when squared, must sum to unity (one).
It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the Born Rule is really just another case of the Pythagorean theorem. The connection is in the way the coefficients of a quantum superposition, when squared, must sum to unity (one). In
In 

 This is the first of a series of posts exploring the mysterious Schrödinger Equation — a central player of quantum mechanics.
This is the first of a series of posts exploring the mysterious Schrödinger Equation — a central player of quantum mechanics. 

 A single line from a blog post I read got me wondering if maybe (just maybe) the answer to a key quantum question has been figuratively lurking under our noses all along.
A single line from a blog post I read got me wondering if maybe (just maybe) the answer to a key quantum question has been figuratively lurking under our noses all along. I posted a while back about the wonders of
I posted a while back about the wonders of 










