It’s been a while since my last Sidebands post. That’s partly because I’ve been working on a project that I’m sure will become a multi-post series and thought it would be nice to start with #81. But I’m not done (or actually started on the writing) yet, and this one has also been lurking for a while.
Essentially, I needed to figure out how to join a cone to a sphere in a seamless way (as in the picture here). This requires the sides of the cone meet the sphere at a tangent point.
It’s yet another case of actually needing the trigonometry I learned in school.
Today (3/14) is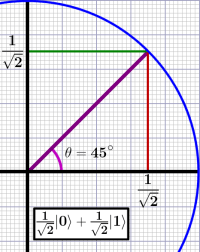 
It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the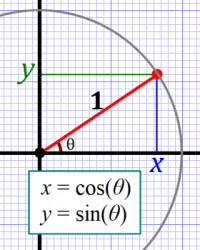 
For me, the star attraction of 
This might seem like another math post… but it’s not! It’s a geometry post! And geometry is fun, beautiful and easy. After all, it’s just circles and lines and angles. Well, mostly. Like anything, if you really want to get into it, then things can get complex (math pun; sorry). But considering it was invented thousands of years ago, can it really be that much harder than, say, the latest smart phone?
Logos con carne 