You may have, at some point, seen one of those bits where a series of seemingly simple math operations somehow end up proving that 1=0 or something equally clearly wrong. Most of them accomplish their joke by sneaking in a hidden division by zero. From that point on, all bets are off (see Divide by Zero).
Recently, on a YouTube channel I follow, I saw a clever example that uses a much sneakier trick. It’s harder to spot because the operation it uses is legit in two of the three possible cases.
The gag, of course, uses the third one.
You may remember learning way back in grade school that you can’t divide by zero. You may remember being told that 
I’ve mentioned before that, after ten years of retired idleness, this year I’ve applied myself to getting some long-standing items off my TODO list. I’m a lazy beaver, not a busy one, but I’ve been less lazy than usual in 2023. (Perhaps, in part, because, on several counts, I can’t believe it’s actually 2023. I remember a time when 2001 seemed far off… in the future.)
This is one of those geeky posts more a “Dear Diary” (or “Dear Lab Notebook”) entry than a post I expect anyone anywhere will get anything out of. This — in part — is about how we define numbers using set theory, so it’s pretty niche and rarified. Tuning out is understandable; this is extra-credit reading.
Or do I mean Logic Square? Because it works either way. The Logic Square (or Square Logic) in question is a logic game created by 
It’s been a while, but the two previous posts in this series (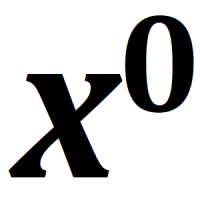
At some point in our early math education, we’re told that anything to the power of zero evaluates to one. 1°=1 and 5°=1 and 99°=1. Basically, x°=1 for all x. It’s typically presented as just a rule about taking anything to the power of zero, but it’s actually derived from a more basic rule about exponents.
I don’t know why I’m so fascinated that the 
Logos con carne 