 So far this week we have Em taking a round-trip to planet Noether at half the speed of light. Upon her return she discovers that, while she’s aged 23.8 years, Al (who stayed home on Earth babysitting Theories) has aged 27. It took her well over twenty years to do it, but Em effectively traveled 3.2 years into the future.
So far this week we have Em taking a round-trip to planet Noether at half the speed of light. Upon her return she discovers that, while she’s aged 23.8 years, Al (who stayed home on Earth babysitting Theories) has aged 27. It took her well over twenty years to do it, but Em effectively traveled 3.2 years into the future.
Last time we saw that — so long as Em is in constant motion — there is symmetry between Al and Em with regard to who is moving and who isn’t. Both can claim the other is (or they are). Both views are valid. Until Em stops. Or starts, for that matter.
Today we look at Em’s “time shadow” — it’s a key to the puzzle!
Let’s start by looking closely at the situation just as Em reaches planet Noether (but while she’s still moving). Here again are the two reference frames:
¶ In Al’s frame of reference (diagram 1), Em travels 6 LY and reaches Noether (cyan dot) when his clock reads 12 years (green dot) — remember that Al slices time horizontally here. (The blue numbers on the left are Al’s years; the green numbers on the right are Em’s.)
Al knows Em’s clock reads 10.4 years because she was moving at relativistic speeds (after all, it’s his Theory, so you’d hope he understands this stuff).
 Notice that, in Al’s frame of reference, Em’s line of simultaneity (slanted green line near top) places Al’s year 9 (purple dot) as simultaneous with Em arriving at Noether.
Notice that, in Al’s frame of reference, Em’s line of simultaneity (slanted green line near top) places Al’s year 9 (purple dot) as simultaneous with Em arriving at Noether.
¶ From Em’s point of view (diagram 2) Al and Earth move away for those 10.4 years (and Noether moves closer). She sees space moving and, therefore, contracted. Al moves 5.2 LY (as she expects), and she knows his clock runs slow due to motion and only reads 9 years (Em also knows the Theory).
Total symmetry of viewpoints. But then Em stops at Noether.
 When she does, she re-enters Al’s frame of reference. In that frame she slices time horizontally just like Al. Suddenly, she’s no longer simultaneous with Al’s year 9 — she’s simultaneous with Al’s year 12!
When she does, she re-enters Al’s frame of reference. In that frame she slices time horizontally just like Al. Suddenly, she’s no longer simultaneous with Al’s year 9 — she’s simultaneous with Al’s year 12!
In diagram 2, Em sliced time horizontally, and we saw Al’s year 9 (green dot) as simultaneous with Em’s year 10.4 (cyan dot). (Al’s line of simultaneity — slanted blue line — put Em’s year 7.79 (purple dot) as simultaneous with him, but that doesn’t matter in this discussion. It’s just part of the symmetry between views.)
 The gray triangle in the diagrams is what I’m calling a “time shadow.” The further away two observers are, the longer the shadow — that is, the further into the past the line of simultaneity extends.
The gray triangle in the diagrams is what I’m calling a “time shadow.” The further away two observers are, the longer the shadow — that is, the further into the past the line of simultaneity extends.
In Em’s case here, at 6 LY going c/2, her light shadow is three years.
At a distance of 12 LY, it’s six years, and at a distance of 18 LY, it’s nine.
You see the pattern. The light shadow is half as long in time as the distance is in light years.
Here’s the crucial point:
When Em changes frames, her simultaneity with Al jumps from his (past) year 9 to his (current) year 12.
But Em has aged only 10.4 years while Al has aged 12.
So long as Em stays on Noether, she and Al share a reference frame (more or less), and their clocks tick in sync — they age at the same rate. Three years go by for both of them, and then Em decides to return to Earth.
She hops on a rocket, and now she’s in a new frame of reference — another moving one, only this one is moving in the other direction, back towards Earth.
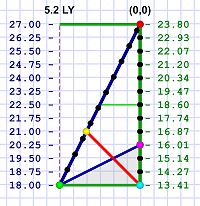
¶ In this new frame (diagram 3), Em’s line of simultaneity is again rotated due to her motion, but this time it’s rotated the other way (because Em is going the other direction). This time the line of simultaneity angles into Al’s future!
 For Al, year 15 (green dot) is three years after Em reached Noether (at age 10.4). They’ve both aged those three years in synch, so Em is 13.4 (cyan dot) when she begins the return trip.
For Al, year 15 (green dot) is three years after Em reached Noether (at age 10.4). They’ve both aged those three years in synch, so Em is 13.4 (cyan dot) when she begins the return trip.
He knows it will take her (from his perspective) 12 years to return, so he knows that will be in his year 27 (15 + 12 = 27). In his frame, Em’s clock runs slower, so she ages only 10.4 years during the trip.
¶ In Em’s frame of reference (diagram 4), her line of simultaneity now crosses Al’s world line in his year 18 — nine years prior to their reunion. Em’s return journey will take the same 10.4 years as did the trip out.
 Em sees that Al is moving (along with Earth and space), so naturally she sees his clock running slower.
Em sees that Al is moving (along with Earth and space), so naturally she sees his clock running slower.
That means it takes Al only 9 years to reach the reunion.
Either way, once they meet, they agree that Al has aged 27 years overall, while Em has aged only 23.8.
§
That’s it. That’s one of the key punchlines of the series. That’s why the Twins Paradox isn’t a contradiction, just an apparent paradox.

Here’s the game changer!
Everything turns on the fact that Em switches frames of reference. She switches to a moving one (and back out) to make the trip out. She switches to another moving one (and back out) to make the trip back. These switches, and the accompanying rotations of lines of simultaneity, are what drives this.
All the groundwork (and I know it was a bit much sometimes) was to support the possibility of fully understanding why Em is now the younger one.
If you don’t, that’s okay. I think everything you need is in the material, but without some background and strong interest, you’d have to treat the series like a textbook and really study it. If it didn’t all sink it, well, that’s probably understandable. I didn’t learn this after one reading, either!
The bottom line is this: Fast enough motion (“relativistic motion”) of a frame we’re observing causes the following things to seem to happen in that frame:
- Length contracts along the line of motion.
- Time dilates (expands); clocks tick slower.
- A number, gamma, quantifies the contraction/dilation.
- (But light-speed always remains constant.)
That’s pretty much the gist of it.
§
 But were not done. There’s a bigger punchline coming with regard to FTL (faster-than-light travel).
But were not done. There’s a bigger punchline coming with regard to FTL (faster-than-light travel).
Astute readers may have already seen it in what I’ve covered. That, and some other final topics, will be for next week.
In the next post I’ll wrap up the relative time discussion and talk about light clocks! As you’ll see, given the way light behaves, the apparent slowing of moving clocks is an absolute necessity!
















And what do you think?