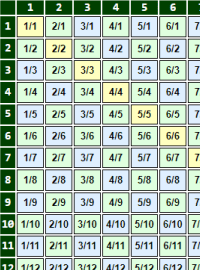
I don’t know why I’m so fascinated that the rational numbers are countable even though they’re a dense subset of the uncountable real numbers. A rational number can be arbitrarily close to any real number, making you think they’d be infinite like the reals, but in fact, nearly all numbers are irrational (and an uncountable subset of the reals).
So, the rational numbers — good old p/q fractions — though still infinite are countably infinite (see this post for details).
More to the point here, a common way of enumerating the rational numbers, when graphed results in some pretty curves and illustrates some fun facts about the rational numbers.
It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the 
In 
I’ve lived with a Beagle, a Keeshond, a Belgian Shepard, a Great Dane, and a Black Labrador. I’ve dog-sat a German Shepard, two Black Labs, and the delightful 
If you know me, or if you’ve followed this blog a while, you know I honor Solar holidays more than human ones. The former are directly linked with the seasons, obviously (and who doesn’t love seasons), but to me they’re about how much (or how little) sunlight we get.
I read 
Logos con carne 