The old saying “Spare the rod, spoil the child” has fallen into, shall we say, severe disfavor these days, even as just a metaphor for strict childrearing. And forget about actually spanking your kid — that’s child abuse by modern standards.
At the same time, we seem to be in the midst of a serious and growing mental health crisis among teens, especially in the USA (but also the UK and Australia).
A new book by Abigail Shrier suggests these may be connected.
The weather has been so weirdly warm this month that I never got around to a Friday Notes for February, so I’m extending the month. Call it a leap year “plus one”. Truth is, I’m at long last finally starting to reach the bottom of my pile. A lot of what’s left is trivial, silly, or outdated, and I may end up doing a thorough spring cleaning on them.
The ultimate goal is for the Notes to be about contemporaneous things rather than from old notes that have been fermenting in the pile.
But for a bit longer, it’ll be a combination of both, so off we go.
My final post in 2023 was about growth curves. It focused on the difference between geometric growth versus exponential growth — which turns out to be not much — and compared them to polynomial growth (see that post for the math-y details; this post isn’t a math post, so relax and read on).
A key characteristic of all these growth curves is that they grow without limit. If we treat the horizontal axis as time, then the longer the growth continues along the curve, the greater whatever growing grows.
The problem is that nothing in the real world can grow infinitely without limit. At some point, something has to give.
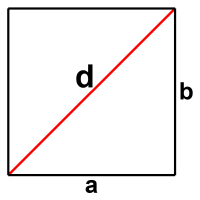Consider the lowly square, a four-sided shape with sides of equal length meeting at right angles. The embodiment of what we’re referring to when we refer to square miles, square kilometers, square inches, or square whatevers. The two-dimensional version of any one-dimensional length.
A trivially easy shape to draw, all you need is a straight edge and a compass — the latter for ensuring your corners are right angles (see Plato’s Divided Line for more on using a straight edge and compass). The only simpler shape is the circle.
Yet the simple square threw early mathematicians into a serious tizzy!
February 15, and winter finally decided show up:
And it’s awfully pretty, I gotta give it that!
An article in a recent issue of New Scientist caught my attention on two counts: firstly, in what it said about my old friend wavefunction collapse and the measurement problem; and secondly, in mentioning Boltzmann Brains. Both set off my “Yeah, but!” reaction.
I’ll touch (as briefly as possible) on the first point, but this little Bubble is mainly about the second one.
Boltzmann Brains bug me.
You may have, at some point, seen one of those bits where a series of seemingly simple math operations somehow end up proving that 1=0 or something equally clearly wrong. Most of them accomplish their joke by sneaking in a hidden division by zero. From that point on, all bets are off (see Divide by Zero).
Recently, on a YouTube channel I follow, I saw a clever example that uses a much sneakier trick. It’s harder to spot because the operation it uses is legit in two of the three possible cases.
The gag, of course, uses the third one.
You may remember learning way back in grade school that you can’t divide by zero. You may remember being told that division by zero is undefined. But have you ever wondered why we can’t divide by zero? Couldn’t the answer just be zero? We get zero when we multiply by zero, so why not when we divide?
But dividing is the opposite (or inverse) of multiplying, so if multiplying by zero gives zero, then maybe dividing by zero gives us… infinity? But infinity isn’t a number (it’s an idea), so that doesn’t work, either.
In this post I’ll dig into why division by zero is undefined.
The first Friday Notes of 2024. (The title nicely caps the 2024, 2023, 2024, 2023 series from the titles of the previous four posts.) We’re well past the glut of holidays, and it’s back to business. There is also the fresh-start sense of the new year. I’m already thinking about all the stuff I want to throw away this coming Spring Cleaning.
My various piles of notes grow smaller and smaller! In some cases, because I deleted notes that seemed to have aged beyond their lifetime. But these Notes posts have been instrumental. In some areas, I’m actually scraping the bottom of the barrel.
But I still have notes, so here we go again…
This post contains the post statistics charts I didn’t have room for in the 2023 wrap-up post. There are a lot of them, and I don’t imagine they’re of much interest to anyone but me. I post them mainly to document the blog. A set of milestones, if you will.
I confess to being fascinated — and utterly befuddled — by which posts receive attention and which little piggies get none. It’s particularly interesting to me when an old post — especially one that never got many views — suddenly gets noticed and sometimes even slightly popular.
Mostly the stats are similar to previous years, but 2023 did bring a few surprises.
Posts pertaining to programming!
Logos con carne 