You may remember learning way back in grade school that you can’t divide by zero. You may remember being told that division by zero is undefined. But have you ever wondered why we can’t divide by zero? Couldn’t the answer just be zero? We get zero when we multiply by zero, so why not when we divide?
But dividing is the opposite (or inverse) of multiplying, so if multiplying by zero gives zero, then maybe dividing by zero gives us… infinity? But infinity isn’t a number (it’s an idea), so that doesn’t work, either.
In this post I’ll dig into why division by zero is undefined.
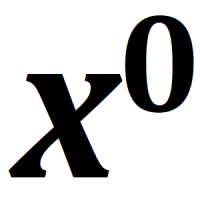At some point in our early math education, we’re told that anything to the power of zero evaluates to one. 1°=1 and 5°=1 and 99°=1. Basically, x°=1 for all x. It’s typically presented as just a rule about taking anything to the power of zero, but it’s actually derived from a more basic rule about exponents.
Yesterday I introduced you to the idea of words as numbers. There are many ways to create a map between words and numbers. For example, we could assign them the number that represents their position in the dictionary. That would make words that start with “A” have smaller numbers while words that start with “Z” would have the largest numbers.
Logos con carne 