Category Archives: Math
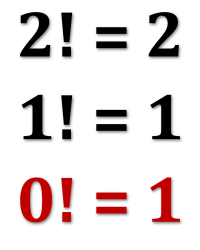 Recently, I learned an interesting new math trick involving what are known as dual numbers. These are compound numbers similar in form to complex numbers but with a different kind of “magic” element enabling their behavior.
Recently, I learned an interesting new math trick involving what are known as dual numbers. These are compound numbers similar in form to complex numbers but with a different kind of “magic” element enabling their behavior.
What makes them interesting to people like me is the surprising way they provide a fast and easy technique for software to generate the derivative of a given function.
As an unrelated bonus, a simple explanation of why zero-factorial is equal to one rather than zero (which might seem more intuitive).
Continue reading
Leave a comment | tags: computer programming, derivatives, dual numbers | posted in Computers, Math
 Time for another Mandelbrot Monday. I’ve mentioned before that aimlessly playing around with Mandelbrot zooms gets old fairly quickly. I find that I do it for a little while, lose interest for a long while, and then pick it up again for a little while.
Time for another Mandelbrot Monday. I’ve mentioned before that aimlessly playing around with Mandelbrot zooms gets old fairly quickly. I find that I do it for a little while, lose interest for a long while, and then pick it up again for a little while.
I’m in the lost interest phase right now — have been for a couple of months. I think I’ll cool my jets until May, when I’m planning a series of posts (“Mandelbrot May”) exploring the Mandelbrot set and how images of it are made.
But I still have images from previous phases to share, so off we go…
Continue reading
Leave a comment | tags: Mandelbrot fractal, Mandelbrot Monday, Ultra Fractal | posted in Math
 One of the Substack blogs I follow, A Piece of the Pi by Richard Green, is almost ideal from my point of view because it features articles that interest me but only — at most — a few a month (so I needn’t strain to keep up).
One of the Substack blogs I follow, A Piece of the Pi by Richard Green, is almost ideal from my point of view because it features articles that interest me but only — at most — a few a month (so I needn’t strain to keep up).
Which matters because keeping up with dozens of science and math blogs, video channels, and occasional papers takes considerable time away from various hobby projects. But sometimes (and this is the third time Mr. Green has done this) something captures my imagination and sends me off on a tangent.
The results often seem worth sharing, and this is no exception. The delight here is that such a simple idea results in a variety of interesting patterns.
Continue reading
5 Comments | tags: computer generated images, Mary Everest Boole, Python | posted in Computers, Math
 This post begins with a bit of what I see as good news. We’re exactly one month away from Winter Solstice — December 21st at 15:03 UTC. That’s 9:03 AM USA Central Time, and I set posts to publish at 9:14 AM, so by the time you read this, it’s just under a month away.
This post begins with a bit of what I see as good news. We’re exactly one month away from Winter Solstice — December 21st at 15:03 UTC. That’s 9:03 AM USA Central Time, and I set posts to publish at 9:14 AM, so by the time you read this, it’s just under a month away.
Cue regular Solstice-Equinox reminder that the day-length changes very slowly at the Solstices and very rapidly at the Equinoxes [cue regular link: Solar Derivative].
Until then, here’s another edition of Friday Notes.
Continue reading
5 Comments | tags: AI, Bentley, eagle, equinox, Python, snow, Solstice, squirrel, weather | posted in Computers, Friday Notes, Math
 For two weeks I’ve indulged in intense 12+ hour days on a self-education project in Python and its Tk module. I plan to write more about that later this week (that’s the plan, anyway).
For two weeks I’ve indulged in intense 12+ hour days on a self-education project in Python and its Tk module. I plan to write more about that later this week (that’s the plan, anyway).
Intense coding and learning take me deep into a Zen-like mindset that’s hard to emerge from. I have a minor self-commitment to publish at least five posts a month but have yet to publish anything this month.
As I struggle to regain the English language, I thought sharing another set of Mandelbrot images offered an easy reentry. The previous post had images from 2019 and 2020. Here are the last of those (and some from 2025).
Continue reading
8 Comments | tags: Mandelbrot fractal, Mandelbrot Monday, Ultra Fractal | posted in Math
 In the Friday Notes from last August, I wrote about needing to buy a new laptop. In the September edition of same, I wrote about installing Ultra Fractal 6 on that laptop and shared a few Mandelbrot images I’d made.
In the Friday Notes from last August, I wrote about needing to buy a new laptop. In the September edition of same, I wrote about installing Ultra Fractal 6 on that laptop and shared a few Mandelbrot images I’d made.
I’ve been sharing two or three in Substack Notes every week for “Fractal Friday”, but Notes is a fast-running river in which things vanish downstream almost instantly.
So, I thought I’d start sharing some here on Mandelbrot Mondays, though I don’t plan to make it a regular thing. I am thinking about a series of posts exploring the Mandelbrot, though.
Continue reading
7 Comments | tags: Mandelbrot fractal, Mandelbrot Monday, Ultra Fractal | posted in Math
 Fall — my favorite season ‘cept for the fading of the light — has fallen here in Minnesota, and our thoughts are turning towards the question of what kind of winter it will be: easy or miserable.
Fall — my favorite season ‘cept for the fading of the light — has fallen here in Minnesota, and our thoughts are turning towards the question of what kind of winter it will be: easy or miserable.
My winter is coming triple mile markers loom, the first dead ahead: Will it snow by Halloween? Will it snow by Thanksgiving? Will it snow by Christmas? Answers to all three vary depending on the whims of Mother Nature and her unexpected offspring, Climate Change.
In the meantime, here we are again for another edition of Friday Notes.
Continue reading
17 Comments | tags: brown sugar, charts, Future Shock, math fun, Quadratic Equation, smoke alarm, stillness, weather | posted in Friday Notes, Math
 It’s been a while since my last Sidebands post. That’s partly because I’ve been working on a project that I’m sure will become a multi-post series and thought it would be nice to start with #81. But I’m not done (or actually started on the writing) yet, and this one has also been lurking for a while.
It’s been a while since my last Sidebands post. That’s partly because I’ve been working on a project that I’m sure will become a multi-post series and thought it would be nice to start with #81. But I’m not done (or actually started on the writing) yet, and this one has also been lurking for a while.
Essentially, I needed to figure out how to join a cone to a sphere in a seamless way (as in the picture here). This requires the sides of the cone meet the sphere at a tangent point.
It’s yet another case of actually needing the trigonometry I learned in school.
Continue reading
3 Comments | tags: cones, POV-Ray, trigonometry | posted in Math, Sideband
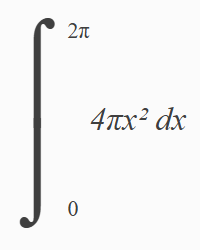 I don’t mean the social kind of integration, which I learned as a child, but the mathematical kind of integration, which I never learned in any of my math classes. I didn’t even take calculus until The Company sponsored some adult education classes for employees.
I don’t mean the social kind of integration, which I learned as a child, but the mathematical kind of integration, which I never learned in any of my math classes. I didn’t even take calculus until The Company sponsored some adult education classes for employees.
But those calc classes only got me through basic derivatives (of polynomials, mostly), so integration has been a bit of a mystery to me. Lately, though, I’ve been trying to pick up the basics.
This post just records my first attempts — my math lab book, so to speak.
Continue reading
3 Comments | tags: calculus, integrals | posted in Basics, Math
 It’s happy hour and you and a friend go out for drinks. The bar is serving a new drink that catches your eye, and you both order one. They’re served in martini glasses (which are upside down hollow cones) and look quite tasty (see picture).
It’s happy hour and you and a friend go out for drinks. The bar is serving a new drink that catches your eye, and you both order one. They’re served in martini glasses (which are upside down hollow cones) and look quite tasty (see picture).
More to the point here, the glasses look acceptably full. Not a lot of “headroom” between the top of the drink and the top of the glass. Your friend, a mathematician, bets you they can pour all of your drink into their glass without spilling a drop.
Should you take that bet?
Continue reading
6 Comments | tags: fun with numbers, cones | posted in Math, Wednesday Wow
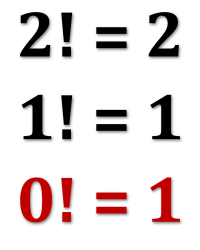 Recently, I learned an interesting new math trick involving what are known as dual numbers. These are compound numbers similar in form to complex numbers but with a different kind of “magic” element enabling their behavior.
Recently, I learned an interesting new math trick involving what are known as dual numbers. These are compound numbers similar in form to complex numbers but with a different kind of “magic” element enabling their behavior. Time for another
Time for another  One of the Substack blogs I follow,
One of the Substack blogs I follow, 
 It’s been a while since my last
It’s been a while since my last 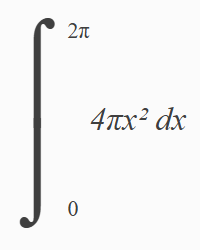 I don’t mean the
I don’t mean the  It’s happy hour and you and a friend go out for drinks. The bar is serving a new drink that catches your eye, and you both order one. They’re served in martini glasses (which are upside down hollow cones) and look quite tasty (see picture).
It’s happy hour and you and a friend go out for drinks. The bar is serving a new drink that catches your eye, and you both order one. They’re served in martini glasses (which are upside down hollow cones) and look quite tasty (see picture).











