Tag Archives: tau day

June 28, 2024

Double Pi(e) Day

Be a Tauist!

I’ve found it extremely difficult to focus this past week. Most of the blame is on Substack Notes, a part of Substack that’s very similar to Twitter or a Facebook feed. I never had Twitter, dumped Facebook ages ago, and barely know what Instagram, Snapchat, et cetera are.

I have no immunity to a doomscrolling feed of interesting micro-posts. Reading them is bad enough. The urge to jump in join the fun is all but irresistible. But days are passing with little to show for them: no books read, no posts worked on, no software projects advanced.

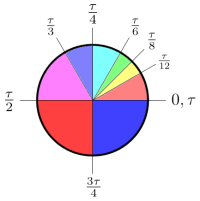
Now it’s Tau Day, and I can’t let that pass postless.

16 Comments | tags: 360 degrees, 60 minutes, circle, Invincible, orbital mechanics, pi, tau, tau day | posted in Baseball, Science, TV

March 14, 2024

BB #92: Actually Using Trig

By Wyrd Smythe

Today (3/14) is Pi Day. People everywhere (or at least math geeks everywhere) are baking decorated pies (or cakes or cookies) to celebrate. And while this is yet another math-y post, it’s not about pi. I’m more of a tau guy, anyway, so I celebrate Tau Day (6/28), because I get twice the (pizza) pie.

Today is also Albert Einstein’s birthday, which I’ve always thought was a cool coincidence. He’s 145 now (and still being widely misquoted).

But this post isn’t about him either.

10 Comments | tags: Albert Einstein, pi day, tau day, trigonometry, two slit experiment | posted in Brain Bubble, Math

June 28, 2019

It’s Tau Day Again

By Wyrd Smythe

Happy Tau Day! It’s funny. I feels like I’ve written a lot of posts about pi plus few about it’s bigger sibling, tau. Yet the reality is that I’ve only ever written one Tau Day post, and that was back in 2014. (As far as celebrating Pi Day, I’ve only written three posts in eight years: 2015, 2016, & 2019.)

What I’m probably remembering is mentioning pi a lot here (which is vaguely ironic in that I won’t eat pie — mostly I don’t like cooked fruit, but there’s always been something about pie that didn’t appeal — something about baking blackbirds in a crust or something).

It’s true that I am fascinated by the number.

3 Comments | tags: Andrey Kolmogorov, Champernowne constant, Gregory Chaitin, Kolmogorov complexity, normal number, normal sequence, omega constant, pi, tau, tau day | posted in Math

March 14, 2016

Happy Pi Day!

By Wyrd Smythe

pi pastry Well, it’s Pi Day once again (although this date becomes more and more inaccurate as the century proceeds). So, once again, I’ll opine that Tau Day is cooler. (see: Happy Tau Day!)

Last year, for extra-special Pi Day, I wrote a post that pretty much says all I have to say about Pi. (see: Here Today; Pi Tomorrow) That post was actually published the day before. I used the actual day to kick off last Spring’s series on Special Relativity.

What remains to be said? Not much, really, but I’ve never let that stop me before, so why start now?

14 Comments | tags: irrational numbers, normal number, pi, pi day, tau, tau day, transcendental numbers | posted in Math

March 13, 2015

Here Today; Pi Tomorrow

By Wyrd Smythe

It’s pi day! Be irrational!

Earlier this week I mentioned that “this coming Saturday is a doubly special date (especially this year).” One of the things that makes it special is that it is Pi Day — 3/14 (at least for those who put the month before the day). What makes it extra-special this year is that it’s 3/14/15— a pi day that comes around only once per century. (Super-duper extra-special pi day, which happens only once in a given calendar, happened way back on 3/14/1529.)

I’ve written before about the magical pi, and I’m not going to get into it, as such, today. I’m more of a tau-ist, anyway; pi is only half as interesting. (Unfortunately, extra-special Tau Day isn’t until 6/28/31, and the super-duper extra-special day isn’t until 6/28/3185!)

What I do want to talk about is a fascinating property of pi.

147 Comments | tags: cake, Carl Sagan, Contact (book), Ellie Arroway, irrational numbers, Magnum Pi, normal sequence, numbers, pi, pi day, pie, real numbers, tau, tau day, transcendental numbers | posted in Math

June 28, 2014

Happy Tau Day!

By Wyrd Smythe

tau-1 This might seem like another math post… but it’s not! It’s a geometry post! And geometry is fun, beautiful and easy. After all, it’s just circles and lines and angles. Well, mostly. Like anything, if you really want to get into it, then things can get complex (math pun; sorry). But considering it was invented thousands of years ago, can it really be that much harder than, say, the latest smart phone?

Even the dreaded trigonometry is fairly simple once you grasp the basic idea that the angles of a triangle are directly related to the length of its sides. (Okay, admittedly, that’s a bit of a simplification. The (other two) angles of a right-angle triangle are directly related to the ratios of the length of its sides, but still.)

However, this isn’t about trig; this is about tau!

10 Comments | tags: circle, circumference, geometry, pi, pi day, pie, pizza, radius, tau, tau day, trigonometry | posted in Math