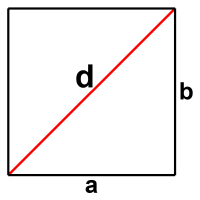
Consider the lowly square, a four-sided shape with sides of equal length meeting at right angles. The embodiment of what we’re referring to when we refer to square miles, square kilometers, square inches, or square whatevers. The two-dimensional version of any one-dimensional length.
A trivially easy shape to draw, all you need is a straight edge and a compass — the latter for ensuring your corners are right angles (see Plato’s Divided Line for more on using a straight edge and compass). The only simpler shape is the circle.
Yet the simple square threw early mathematicians into a serious tizzy!
It’s actually obvious and might fall under the “Duh!” heading for some, but it only recently sunk in on me that the 
This week I’ve focused on the relativity of time under motion, and we’ve seen that moving very fast allows “time travel” into the future. Very handy if you don’t mind the one-way trip. What’s more, a spaceship capable of such a flight is physically possible, so it’s a “time machine” we know works!
Logos con carne 