Tag Archives: fun with numbers
It’s happy hour and you and a friend go out for drinks. The bar is serving a new drink that catches your eye, and you both order one. They’re served in martini glasses (which are upside down hollow cones) and look quite tasty (see picture).
More to the point here, the glasses look acceptably full. Not a lot of “headroom” between the top of the drink and the top of the glass. Your friend, a mathematician, bets you they can pour all of your drink into their glass without spilling a drop.
Should you take that bet?
Continue reading
6 Comments | tags: cones, fun with numbers | posted in Math, Wednesday Wow
In the last post, I mentioned a simple logic puzzle that I’d stumbled over while wandering around the interweb. Start with four glasses, in a row, all upright. The goal is, through a series of moves, to turn them all upside down. On each move, you flip three of the four glasses — up if down or down if up.
The goal is to end up with all four glasses upside-down in the least number of moves possible. It’s not hard to find the solution by trial and error, but it turns out there’s an underlying trick that not only solves it but solves it regardless of the number of glasses (where each move flips N-1).
Bonus: these solutions even look pretty — or at least symmetrical.
Continue reading
11 Comments | tags: fun with numbers, logic games, logic puzzle | posted in From My Collection
Earlier this year, I posted about that math gag that seems to prove (very mathematically) that 2=0 (an alternate version “proves” 1=0 using the same trick: a covert division by zero, an operation whose undefined result breaks the chain of logic).
Today I’m posting about another somewhat common mathematical (or rather, geometrical) gag — one involving chocolate! In the form of a magical chocolate bar that lets us remove an infinite number of bite-sized pieces but somehow remains the same size. It seems impossible.
And of course, it is. In this post I reveal the magician’s trick!
Continue reading
22 Comments | tags: chocolate, fun with numbers, geometry, old tricks, triangle, tricks | posted in Math
You may have, at some point, seen one of those bits where a series of seemingly simple math operations somehow end up proving that 1=0 or something equally clearly wrong. Most of them accomplish their joke by sneaking in a hidden division by zero. From that point on, all bets are off (see Divide by Zero).
Recently, on a YouTube channel I follow, I saw a clever example that uses a much sneakier trick. It’s harder to spot because the operation it uses is legit in two of the three possible cases.
The gag, of course, uses the third one.
Continue reading
7 Comments | tags: fun with numbers, imaginary unit, numbers | posted in Brain Bubble, Math
And the total is…?
Oh the irony of it all. Two days ago I post about two math books, at least one of which (if not both) I think everyone should read. This morning, reading my newsfeed, I see one of those “People Are Confused By This Math Problem” articles that pop up from time to time.
Often those are expressions without parentheses, so they require knowledge of operator precedence. (I think such “problems” are dumb. Precedence isn’t set in stone; always use parentheses.)
Some math problems do have a legitimately confusing aspect, but my mind is bit blown that anyone gets this one wrong.
Continue reading
10 Comments | tags: fun with numbers, math phobia, mathematics | posted in Math, Rant, Society
There are many science-minded authors and working physicists who write popular science books. While there aren’t as many math-minded authors or working mathematicians writing popular math books, it’s not a null set. I’ve explored two such authors recently: mathematician Steven Strogatz and author David Berlinski.
Strogatz wrote The Joy of X (2012), which was based on his New York Times columns popularizing mathematics. I would call that a must-read for anyone with a general interest in mathematics. I just finished his most recent, Infinite Powers (2019), and liked it even more.
Berlinski, on the other hand, I wouldn’t grant space on my bookshelf.
Continue reading
11 Comments | tags: calculus, David Berlinski, derivatives, fun with numbers, integrals, numbers, Steven Strogatz, The Joy of X | posted in Books, Math
In recent posts I’ve presented the complex numbers and the complex plane. Those were just stepping stones to this post, which involves a basic fact about the Mandelbrot set. It’s something that I stumbled over recently (after tiptoeing around it many times, because math).
This is one of those places where something that seems complicated turns out to have a fairly simple (and kinda cool) way to see it when approached the right way. In this case, it’s the way multiplication rotates points on the complex plane. This allows us to actually visualize certain equations.
With that, we’re ready to move on to the “heart” of the matter…
Continue reading
22 Comments | tags: cartioid, complex numbers, fun with numbers, Mandelbrot, Mandelbrot fractal, real numbers | posted in Math
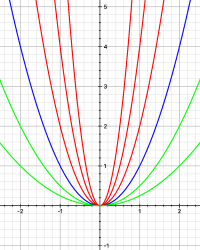
Graph of ax2 for diff a values.
(green < 1; blue = 1; red > 1)
This is a little detour before the main event. The first post of this series, which explained why the imaginary unit, i, is important to math, was long enough; I didn’t want to make it longer. However, there is a simple visual way of illustrating exactly why it seems, at least initially, that the original premise isn’t right.
There is also a visual way to illustrate the solution, but it requires four dimensions to display. Three dimensions can get us there if we use some creative color shading, but we’re still stuck displaying it on a two-dimensional screen, so it’ll take a little imagination on our part.
And while the solution might not be super obvious, the problem sure is.
Continue reading
12 Comments | tags: complex numbers, fun with numbers, imaginary unit, numbers, parabola, real numbers, x-squared | posted in Math
Yes, this is a math post, but don’t run off too quickly. I’ll keep it as simple as possible (but no simpler), and I’ll do all the actual math so you can just ride along and watch. What I’m about here is laying the groundwork to explain a fun fact about the Mandelbrot.
This post is kind of an origin story. It seeks to explain why something rather mind-bending — the so-called “imaginary numbers” — are actually vital members of the mathematical family despite being based on what seems an impossibility.
The truth is math would be a bit stuck without them.
Continue reading
23 Comments | tags: complex numbers, complex plane, fun with numbers, imaginary unit, integers, Leopold Kronecker, natural numbers, numbers, rational numbers, real numbers | posted in Math
Logos con carne 