Category Archives: Science
Complete Chaos!
One of my favorite discoveries in life is the Mandelbrot set. Considering it gives me a strong sense of the numinous. I’ve been enthralled by it ever since Fractint, an MS-DOS program that generated fractals. I’ve posted about it a lot here; today I want to take you into the heart of its chaotic behavior.
The Mandelbrot set has a number of properties that make it such a fascinating study: Firstly, it demonstrates chaos theory. Secondly, it demonstrates how complex patterns can arise from simple beginnings. Thirdly, it reveals a problem concerning real numbers. Fourthly, every pixel is a demonstration of Turing’s Halting Problem. It’s also infinitely complex and incredibly beautiful.
Today we’re going to explore the shore of the Mandelbrot lake.
Continue reading
7 Comments | tags: chaos, chaos theory, fractals, Mandelbrot, Mandelbrot fractal | posted in Science
I’ve written before about Drake’s Equation and the Fermi Paradox. The former suggests the possibility of lots of alien life. The latter asks okay, so where the heck are they? Given that the universe just started, it’s possible we’re simply the first. Maybe the crowd comes later. (Maybe we create the crowd!)
Recently, one of my favorite YouTube channels, PBS Space Time, began a series of videos about this. The first one (see below) talks about the Rare Earth Hypothesis, a topic that has long fascinated me.
The synchronicity in this is that I’d just had a thought about basic probability and how it applies to our being here…
Continue reading
16 Comments | tags: alien contact, alien races, alien vistors, aliens, ancient alien races, ancient aliens, anthropic principle, Drake Equation, Fermi Paradox, PBS Space Time, Rare Earth Hypothesis | posted in Opinion, Science
There is something about the articles that Ethan Siegel writes for Forbes that don’t grab me. It might be that I’m not in the target demographic — he often writes about stuff I explored long ago. I keep an eye on him, though, because sometimes he comes up with a taste treat for me.
Such as his article today, No, Thermodynamics Does Not Explain Our Perceived Arrow Of Time. I jumped on it because the title declares something I think many have backwards: the idea that time arises from entropy or change. Quite to the contrary, I think entropy and change are consequences of time (plus physics).
Siegel makes an interesting argument I hadn’t considered before.
Continue reading
62 Comments | tags: arrow of time, entropy, Ethan Siegel, got time, is time fundamental, laws of thermodynamics, thermodynamics, time | posted in Opinion, Physics
Recently, I’ve been involved in some discussions about causality, and some of those discussions have struggled to find any resolution, which I find frustrating. I don’t think people need to agree on ideas, but my experience is that usually people can agree on how to frame and talk about those ideas.
I sometimes get the feeling people are so set on disagreeing that they don’t always engage on what the other party is saying. I never know if it’s a lack of comprehension, a lack of willingness, or (on my part) a lack of communication skill or sufficient explanation.
So here are some things I think (I hope) are uncontroversial.
Continue reading
10 Comments | tags: causal determinism, causal system, causality, determinism, electricity, physical system, sound vibrations, sound waves | posted in Science
Recently I had a debate with someone who was downright evangelical about the Block Universe (BU) being, absolutely, positively, the way things are. Because Special Relativity. In particular because of what SR says about simultaneity between inertial frames.
Up to that point I’d never given the BU a great deal of thought other than to file it under «Probably Not the Case» (for reasons I’ll get to). But during my morning walks I’ve turned it over in my mind, and after due consideration… I still think it’s probably not the case.
I get why people feel SR seems to imply a BU, but I don’t see the necessity of that implication. In fact, it almost seems contrary to a basic tenant of SR, that “now” is strictly a local concept.
Continue reading
15 Comments | tags: block universe, line of simultaneity, plane of simultaneity, simultaneity, simultaneous events, spacetime, Special Relativity, surface of simultaneity, time-space diagram | posted in Physics
Musicians practice; actors rehearse; athletes work out; and mathematicians play with numbers. Some of the games they play may seem as silly or pointless as musicians playing scales, but there is a point to it all. That old saying defining insanity as doing the same thing over and over and expecting different results was never really correct (or intended to be used as it often is).
An old joke is more on point: “How do you get to Carnegie Hall?” (Asked the first-time visitors to New York.) — “Practice, practice, practice!” (Replied the street musician they asked.) The point of mathematical play can be sheer exercise for the mind, sometimes can uncover unexpected insights, and once in a while can be sheer fun.
As when finally solving a 65-year-old puzzle involving the number 42!
Continue reading
8 Comments | tags: 42, Andrew Booker, Diophantine equation, discrete mathematics, mathematics, Numberphile | posted in Math
I have always liked those comparisons that try to illustrate the very tiny by resizing it to more imaginable objects. For instance, one says: if an orange were as big as the Earth, then the atoms of that orange would be a big as grapes. Another says: if an atom were as big as the galaxy, then the Planck Length would be the size of a tree.
The question I have with these is: How accurate are these comparisons? Can I trust them to provide any real sense of the scale involved? If I imagine an Earth made of grapes, am I also imagining an orange and its atoms?
So, I did a little math.
Continue reading
20 Comments | tags: atomic nucleus, atoms, carbon, electrons, orange, Planck Length, protons | posted in Science
In the last week or so I read an interesting pair of books: Through Two Doors at Once, by author and journalist Anil Ananthaswamy, and The Order of Time, by theoretical physicist Carlo Rovelli. While I did find them interesting, and I’m not sorry I bought them (as Apple ebooks), I can’t say they added anything to my knowledge or understanding.
I was already familiar with the material Ananthaswamy covers and knew of the experiments he discusses — I’ve been following the topic (the two-slit experiment) since at least the 1970s. It was nice seeing it all in one place. I enjoyed the read and recommend it to anyone with an interest.
I had a little trouble with the Rovelli book, perhaps in part because my intuitions of time are different than his, but also because I found it a bit poetic and hand-wavy.
Continue reading
25 Comments | tags: Anil Ananthaswamy, arrow of time, Carlo Rovelli, is time fundamental, light, photons, Planck Length, Planck Time, spacetime, time, two slit experiment | posted in Books, Physics
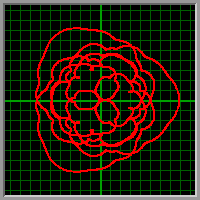
Fourier Curve 1
Don’t let the title put you off — this is one of the coolest things I’ve seen in a while. It’s because of math, but there’s no need to get all mathy to enjoy this, you just need to think about clocks. Or even wheels that spin ’round and ’round.
The fun thing is what happens when we connect one wheel to another in a chain of wheels of different sizes and turn rates. If we use the last wheel to trace out a pattern, we get something that resembles the Spirograph toy of old (which worked on a similar principle of turning wheels).
And if we pick the wheel sizes and spin rates just right, we can draw just about any picture we want.
Continue reading
4 Comments | tags: 3Blue1Brown, JPEG, sine wave | posted in Math, Wednesday Wow
I’ve long been fascinated by stories about octopuses. I confess I’ve eaten a few, too, and it’s obviously a worse than eating dog, which I could never. (OTOH, properly done calamari is really yummy!)
It’s not just that octopuses (and it is octopuses, by the way; the root is Greek, not Latin) are jaw-dropping smart. It’s that their intelligence operates in a completely different brain than ours — an evolutionary branch that considerably predates the dinosaurs. It isn’t just the top brain and eight satellite brains; it’s that their entire body, in some sense, and especially their skin, is their brain.
Check out this 13-minute TED Talk by marine biologist Roger Hanlon:
Continue reading
46 Comments | tags: brain, intelligence, mind, octopus | posted in Science
Logos con carne 