Mandelbrot Monday

In the Friday Notes from last August, I wrote about needing to buy a new laptop. In the September edition of same, I wrote about installing Ultra Fractal 6 on that laptop and shared a few Mandelbrot images I’d made.

I’ve been sharing two or three in Substack Notes every week for “Fractal Friday”, but Notes is a fast-running river in which things vanish downstream almost instantly.

So, I thought I’d start sharing some here on Mandelbrot Mondays, though I don’t plan to make it a regular thing. I am thinking about a series of posts exploring the Mandelbrot, though.

As I mentioned in September, Mandelbrot zooms are fun for a while but get old quick for me. That’s already happening a bit, but I have a collection of over 120 so far and can keep posting them for a while even if I make very few more.

What I have been doing more of is exploring the various nooks and crannies of the Mandelbrot, and I think that might keep me going for a while, especially if I start writing about it.

But enough wyrds, on with the show, and let’s begin with the star of the show, the Mighty Mandelbrot:

The actual Mandelbrot set comprises the black area in the “main cardioid”, its many “circular bays”, its endless mini-brots (three are visible above) and the threads and filaments that surround the boundary zone.

Note that all points in the Mandelbrot set are simply connected, which means there are no holes in the black area, and you can reach any point from any other point while staying in the black area. Topographically, we can deform the Mandelbrot into a disc with all points inside the disc.

In most images, the points inside the Mandelbrot set are colored black, as you’ll see in all these images. Points outside — points not in the set — are colored for the interesting effects seen in most renderings, and there are many approaches to that coloring. The traditional one involves using the number of iterations it takes for the point to “escape” (be shown to not be in the set). I used that coloring technique for everything here (except for the last).

Here’s a different rendering of the same thing to help orient ourselves:

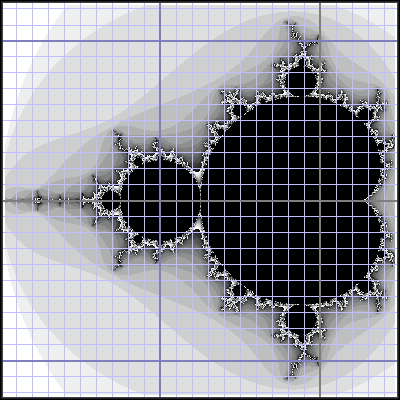
We’re on the complex plane. The X axis runs horizontally across the middle of the image. The Y axis is the thick vertical line towards the right. The thick vertical line in the middle-left is the -1 point on the X axis. The thick horizontal lines running across the top and bottom are the +1 and -1 points on the Y axis, respectively.

The entire Mandelbrot lives between X=-2.0 to +0.5 and Y=-1.25 to +1.25. Call it 2.5 units wide and high. All the interesting stuff lies along the border between the inside and outside. From a purest sense, there really are only two colors because all points are either inside or outside the set.

The zooms below are clickable for a large-size version (3840×2160). If you find these interesting, I recommend spending some moments with the larger versions and studying the fine details of the images.

Starting back in the image library, the first four are from November of 2019 (when I had UF loaded on my Dell laptop; I never loaded it on the HP I had after the Dell crapped out):

x=+0.365441237406898537275634464919826944709
y=+0.3627982558619870213261499227436402711285
magnification=3.5491865e28

The palette uses hard edges between colors to generate that wheel-in-a-wheel effect. Much of the fun of these Mandelbrot images is playing with the color palette (which can be done in a variety of ways).

I call this one Lightning Brot:

x=+0.1801494095943112456800735182
y=+0.56279776297307378534342805915
magnification=1.0709222e18

There are two distinguishing characteristics with these:

Firstly, there is the primary structure around the mini-brot. In this case, it has a branching structure somewhat similar to lightning. The structure here reflects the neighborhood of the last mini-brot we zoomed past.

Secondly, the structure surrounding, the “outside” structure. This reflects the structure of the Mandelbrot at the specific X and Y coordinates of the zoom. In this case, it has the “eye” structure found close to the boundary of the main cardioid.

In this one, that “eye” pattern is prominent and reflects the local neighborhood:

x=+0.3350943551672631895433387
y=+0.06728395278272029148180005
magnification=5.2983523e14

In this one, the primary structure is the “eye” shape. There isn’t much to see of the surrounding structure, but the coordinates tell me we’re on the right-hand boundary.

Here’s a little change of pace:

x=-1.47468225698589338669535732179902545
y=+0.000000014840551434975421638941496201361056
magnification=2.8930339e25

Lots of places down in the Mandelbrot have square shapes! There are octagons, also. Generally, patterns in the Mandelbrot come in powers of two.

The next three are from December of 2019.

Another common pattern involves a “dumbbell” shape:

x=-1.44771053828558920458496322849709978
y=-0.0001277717432724636863147640094165237735
magnification=9.4057151e25

This being a fractal, notice how each dumbbell had a dumbbell inside, and the little “eyes” on those inner dumbbells are also dumbbell shapes (and so on). Zooming in on the little piece in the center eventually leads to another mini-brot.

The dumbbell shape comes into play with the Halloween Mandelbrot zooms I made (as you’ll see below).

Here’s another squarish shape:

x=-0.16092949623778197722602211618467179550983433303700…
y=+1.03657955547683141009969876248399122171233485009790…
magnification=4.3162954e54

In the large version, check out the colorful spirals. Note the larger magnification on this one — 10⁵⁴. At this depth, there isn’t room for all the digits in the X and Y coordinates.

Yet it’s still very shallow as zooms go. I’ve seen them as deep as 10²¹⁸³¹ (the current record holder to the best of my knowledge). That one comprises eleven videos, each over two hours long. Twenty-two plus hours of zooming and zooming and zooming…

[Here’s a link to a playlist if you’re curious.]

Last one from 2019:

x=-0.7493646003468487277348783
y=-0.089024826622409910920679095
magnification=1.6392188e15
angle=-61.017

This is something of a variation on the dumbbell shape. Related, anyway. I love the “mesh” of paths (I think I’ll call this Mandel Mesh). The lines of the mesh are quite intricate in the full-size image.

I don’t usually rotate zooms unless there’s a good reason, but I wanted this one horizontally oriented, so we’re rotated a bit over 60 degrees here.

Now three from 2020.

I call this one Snowflake for obvious reasons (although its symmetry is eight-fold rather than six-fold):

x=+0.2500762716952646157604745657845056497561
y=+0.00000095376270787816059145030278941664853098295
magnification=6.0110601e30

Note the Y coordinate — we’re very close to the real axis. The X coordinate indicates we’re right in the Mandelbrot’s butt crack.

x=+0.26557175385299295977317512431045
y=+0.0029724527621191566863238539335865
magnification=5.245952e20
angle=30.3164

Another one I rotated to get a horizontal orientation. I like the general fuzziness of this one. Looks organic.

It’s also an example of mathematical chaos because, despite the very small area involved, the pixels change a lot over that area (all the small detail in the image). The only difference between pixels is their coordinates, and very tiny changes in the X and Y of those coordinates results in very different escape iterations (which results in the different colors).

Last one from 2020:

x=-1.9918934524827294831410957483787903682667338877713…
y=+0.0000007516730693282685718838419194637761173475790…
magnification=3.2737658e85

This is the deepest one so far in this post: 10⁸⁵. The actual X and Y coordinates are much too long to fit. Both have over 100 decimal digits. Note the X coordinate, though. We’re way out near the tip of the needle, nearly to -2.0 on the X axis. That’s why the structure looks like it does.

What’s interesting about any zoom that goes above 10⁶⁵ is that if each pixel in the zoom is considered to measure one Planck length on a side, then the full Mandelbrot would be larger than the visible universe. The deeper zooms imply a Mandelbrot much, much larger than that.

Earlier this month, I made some Halloween-themed zooms. I call this one Surrounded by Ghosts:

x=-1.02651064440710311807027990285471803114
y=+0.360889650643563437558813801486703806901
magnification=9.1652481e28

It’s one of my favorites in this lot. Check out the detail in the large version! This one makes use of an eight-fold dumbbell pattern, and of course the ghost eyes are dumbbells, too.

This is Spider Pumpkin:

x=-1.027534850577444749228839987
y=+0.38804111800610339752068715065
magnification=2.5859781e18

The eight-fold symmetry works out nicely for spiders.

This is Ghost Dance:

x=-1.02753485057744474918775744176035094372215
y=+0.388041118006103397538174086643675879830165
magnification=6.8868527e30
angle=57.4609

Although maybe I should call it Ghost Eye.

This is Spider Goblins:

x=-1.0275348505774447492173494715105088356
y=+0.388041118006103397526323147961466564045
magnification=1.2635435e28
angle=-57.3047

The dumbbell pattern, this time with double-pupil green eyes and branching grasping clawed arms.

Here’s the penultimate one for today:

x=-1.027534850577444749217349471510328841686185
y=+0.3880411180061033975263231479616855720953665
magnification=1.7108237E32
angle=-100.0237

Goblins again. Note the square shape with dumbbell heads in each corner (and each head has dumbbell eyes with dumbbell double-pupils). Not sure what to call this yet. Goblin Coven, maybe? But a coven should be three or maybe thirteen and should have witches.

I’m open to suggestions.

Lastly, something rather different:

x=-1.586849652059159471
y=0.0014986200325571018025
magnification=4.4119609e10

This is still a Mandelbrot zoom, but it uses a different algorithm for coloring the outside points. All the previous images — nearly all the zooms I make — use the traditional coloring algorithm. That is, the number of iterations required for the point to escape determines the point’s color. Within that technique there are still variations besides the color palette itself.

The image above uses what’s called Direct Orbit Traps. As you see, the algorithm results in very different images. This is the first time I’ve started to explore alternate coloring algorithms. Many of them don’t do much for me (or more likely I don’t know how to use them effectively), but I do like orbit traps. Somehow, they make the image look like candy.

§ §

And on that note, that’s all for now. I’ll post more down the road.

Stay fractal, my friends! Go forth and spread beauty and light.

∇