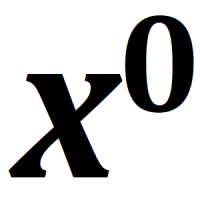At some point in our early math education, we’re told that anything to the power of zero evaluates to one. 1°=1 and 5°=1 and 99°=1. Basically, x°=1 for all x. It’s typically presented as just a rule about taking anything to the power of zero, but it’s actually derived from a more basic rule about exponents.
Thinking about x° in connection with something else recently, it occurred to me there’s a second way to justify the notion that anything to the power of zero is one.
It also occurred to me 0ⁿ might be an implementation of the Dirac delta.
Logos con carne 