For two weeks I’ve indulged in intense 12+ hour days on a self-education project in Python and its Tk module. I plan to write more about that later this week (that’s the plan, anyway).November 17, 2025 2:08 pm
For two weeks I’ve indulged in intense 12+ hour days on a self-education project in Python and its Tk module. I plan to write more about that later this week (that’s the plan, anyway).
Intense coding and learning take me deep into a Zen-like mindset that’s hard to emerge from. I have a minor self-commitment to publish at least five posts a month but have yet to publish anything this month.
As I struggle to regain the English language, I thought sharing another set of Mandelbrot images offered an easy reentry. The previous post had images from 2019 and 2020. Here are the last of those (and some from 2025).
Not that I’m sharing them all — they aren’t all that interesting. There is some sense of repetition as well. Someday, I’ll post share them all on my personal website (along with all my Python code), but that’s a project for the future.
My fascination with the Mandelbrot goes back to the MS-DOS days in the late 1980s and an ancient program called FRACTINT.EXE (it was so old that we hadn’t invented lowercase letters for computers yet). It implemented the necessary arbitrary precision math at the assembly level so generated fractal images as fast as anything ordinary people had access to in 1988.
My buddy and I often spent hours waiting for it to draw a single image. In only 256 colors. At very shallow zoom depths. And yet it was amazing. The more I learn about it, the more amazing the Mandelbrot is. From an abstract maths point of view as well as from an artistically stunning point of view. Beauty combined with something very deep and abstract about math (and thus, one presumes, about reality).
The Mandelbrot set is quintessentially a computational (thus abstract) object. It has an algorithmic definition — it cannot be evaluated; it must be computed. [See Computation vs Evaluation] And yet, paradoxically, it can never be fully computed because each pixel is a Turing Halting Problem. The set is well-defined mathematically but can never be actualized. Only computed to some resolution (some thinkers believe things like this, and in general the Halting Problem and the Gödelean incompleteness that underlies it, disprove the Simulation Hypothesis).
There’s a lot packed into a Mandelbrot, is what I’m saying.
And having said all that, off we go. As always, I recommend downloading them and using a good image viewer to see them in their full-sized 3840×2160 glory. As they say, Heaven is in the details, and that is surely true of these.
x=-0.774554148338033867825765 y=-0.12453226483536051606771 magnification=8.7051193e12 angle=30.0246
From, interestingly enough, November 18, 2019. Almost exactly 6 years ago. It uses the same color palette as the fourth one from last time but isn’t related in terms of coordinates. I rotated it to line it up with the frame. I like the lacey outer parts and fiery corona around the green lagoon.
x=-1.479766095034192427681845674405594488974944908 y=-0.0004401585382715275723721030467218944455639347514 magnification=1.6378152e36
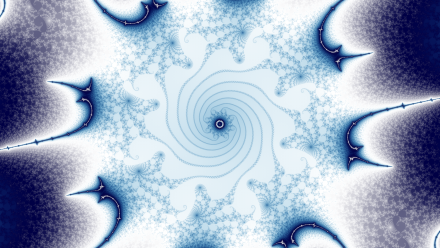
This and the next three are all from December of 2019. I call this one Spiraling In for obvious reasons. So many spirals. The big central spiral is a genuine spiral. There are places that look like spirals — mostly because of the color palette used — but in fact the outside paths go relatively straight towards the center.
Remember that the Mandelbrot set is fully connected so no matter how deep one zooms, the outside always winds down into it. The green-gold solid areas on the edges are the outside. We’re zoomed down to 1.6e36 but could follow the outside here all the way up to the border and beyond.
x=-0.72576848730249390921912640487144 y=-0.240241592527613463784302424183025 magnification=7.7896926e22
I usually prefer more subtle color palettes, but the green/purple works here, I think. The 16 big “lobster” shapes surrounding the mini-brot in the center are a common formation in these zooms. Note the 32 smaller purple “lobsters” in the inner ring. I especially like how their “tails” seem to create vortexes moving off behind them. The fine detail looks a bit like seaweed, enhancing the sense of lobsters.
x=-0.74936460034684871882722456655 y=-0.08902482662240990760399883935 magnification=1.7794325E18 angle=15.4001
This is a slightly deeper zoom of the seventh one from last time and looks very similar except this one has a four-way symmetry compared to the other one’s two-way symmetry. I like the sense of a net these have as well as the lacey outside.
x=-1.770713669680077930525305824082 y=+0.063903485086232294547580493023865 magnification=2.4822426e21
I call this one Running Around in Circles. Note again how the outer motif of 16 “legs” is repeated inside with 32. The branchy structure here is rather different from the lacey structures seen in others. It has to do with where the zoom starts on the main Mandelbrot. It’s also affected by zooming close to mini-brots. (This is all part of what I hope to explore in more detail in a series of posts focusing on the Mandelbrot itself.)
Now we jump into January of 2020:
x=-1.31483536774706000456086518619 y=+0.07298935212951235911817045431455 magnification=2.6133603e19
This is one of my favorites (though it could use a better color palette, I think). I love the “scary forest” branching structure here. It comes from zooming close to the boundary along the main cardioid.
x=-1.4797648308116962172754718203885 y=+0.000321500057020231550714080629140155 magnification=4.3705218e22
Same day but different location and a very different structure. More spirals!
I think this one might be called Crazy Eyes. Reminds me a bit of the crazy eyes emoji (😵💫).
x=+0.270184671178852475099492475690318963126895 y=+0.0041843414727977169485093743421308434985579 magnification=1.6627779e31 angle=79.847
Last one from 2020. A study in green-blue. Not spectacular but it has an interesting shape with some nice filigree. Rotated to align with the frame (these all have a 16×9 aspect ratio; I use them for active wallpaper slideshow on my 60″ TV sometimes).
x=unknown y=unknown magnification=unknown
Based on the filename, this is apparently from September 19th of this year, which would be shortly after I installed Ultra Fractal on my new laptop. I had grown a bit tired of Mandelbrot zooms back in 2020 so never installed it on my last laptop. For whatever reason, I started thinking about the Mandelbrot again and so installed UF on this one.
Been enjoying it, but I think it’s main utility will be in providing examples for a series of posts about the Mandelbrot. Maybe next March or May will be Mandelbrot Month.
But, more to the point, on this one I didn’t record the parameters nor save them. I have no idea how deep it is, but it looks like a deep one. Appropriately jarring color palette, too.
One thing that happens in deep zooms is that the radial frequency (which is always in powers of two) gets very large.
I also don’t have parameters for this one or the next three. I only know from their filenames that I created in September. I made these kind of off-the-cuff for Substack Notes. They’re atypical in their structure, which seems much more organic than I usually see. Looks a lot like an island to me, though I’m not so sure about the surrounding waters.
A deeper zoom of the same location but a very different color palette. Doesn’t look so much like an island anymore but still has that weird almost amorphous shape of the last one.
Stand by for a major change of pace:
This one looks almost evil. The color palette has a lot to do with it — dark and moody, a study in black and brown. Another off-the-cuff one I made for Substack.
(FWIW, I’m posting three Mandelbrot images on Substack every Friday for “Fractal Friday”. See my Notes feed.).
One Substackian found it so disturbing that I made a less evil one for him:
Which is actually just a bit deeper in the same location, but I added green to the color palette to make it friendlier. Note the same claw-like motif to the structure, though.
I also like the horizontal nature of it. No doubt I rotated it to align it. I like the marching army of “boots” around the borders, too. While I find the evil one above very compelling, I like this one better.
x=+0.2617331068522581094379944415 y=+0.00190887140180981147845359632 magnification=1.1442952e18 angle=90
I call this one Looking at You, and it somehow reminds me of a hedgehog. A strangely colored mathematical computer hedgehog, but a hedgehog, nevertheless.
And I’d gotten back to being more careful about recording parameters or saving the fractal settings. I even wrote some Python code to go through those Ultra Fractal file and extract the parameters into a JSON file, which is how I’m able to provide them here.
x=+0.27971376828231765135607465632616637067725 y=+0.0084336491254680377550414851975425111383255 magnification=7.8900231e31
I used this color palette a little too often and can barely stand it now, but I like the image. I may someday re-render it in a different palette. I’m tempted to call this one Mandel-Tron because it reminds me of the ships in Tron (1982), but I’ve got other images that are even more evocative of those ships.
x=+0.2797137682823176513560746563261668087069511815 y=+0.0084336491254680377550414851975412362172059962775 magnification=9.5513308e35
A deeper zoom in the same location (with that same color palette, ugh). But I do like the lacey details, though. The “fishhook” shapes are indicative of zooming into the “needle” of one of the mini-brots. The coordinates of this one put it on the eastern border (as far from the main needle as possible), so these are from a mini-brot I zoomed past.
It’s stuff like this that I want to explore in the posts I’m planning along with some details about the Mandelbrot itself.
x=+0.27971376828231765135607465632616680870649082294365 y=+0.0084336491254680377550414851975412362170763265432485 magnification=6.0021862e38
And an even deeper zoom to find the mini-brot that lurks down within. Note how all three of these last ones repeat the basic structural motif but at increasingly higher radial frequencies. There’s also a strong spiral structure to these that I like.
Last time I ended with a bonus Mandelbrot fractal using a different coloring algorithm for the outside. I’ll end this time with a different different coloring algorithm:
x=0.3968177745984 y=0.60422518326245 magnification=836.0859
I can’t say I much care for this one, but it’s interesting to see what other options there are for coloring the rendering. As you can see, this isn’t a deep zoom, just 800+ to find a mini-brot as a centerpiece for the coloring algorithm.
As is usually the case, the inside — the points inside the Mandelbrot set — is colored black, though there are coloring algorithms for the inside, too. Most Mandelbrot renderings color the outside — the points that have escaped. The coloring algorithm uses some aspect of their calculation to determine how to color the pixel.
The traditional method uses the count of iterations — how long the equation cycled before the point “escaped”. That count can be process through various math operations (square root, cube root, log, etc) to change how the palette responds.
Non-traditional methods use some other aspect of the calculation. I haven’t explored this too deeply, so I don’t feel competent to talk about it (yet).
§ §
And on that note, I’ll end for now. Definitely more to come. And now I have at least one post out this month. Time to get cracking on some more.
Stay Mandel-isous, my friends! Go forth and spread beauty and light.
∇
Posted by Wyrd Smythe
Categories: Math
Tags: Mandelbrot fractal, Mandelbrot Monday, Ultra Fractal
Mobile Site | Full Site
Get a free blog at WordPress.com Theme: WordPress Mobile Edition by Alex King.
Haunting. Disturbing. Especially with a soundtrack. Such as, “I don’t care anymore” Phil Collins. 🍻
By Mark Edward Jabbour on November 17, 2025 at 2:31 pm
There ya go! 😊
By Wyrd Smythe on November 17, 2025 at 2:49 pm
That last one looks something like what I imagine a black hole would look like. A couple of them remind me of geodes. The one you made for the friend who found the other ones disturbing looks like it would make a great belt design, or maybe a choker-type woman’s necklace. I really love these. They are so unusual and so beautiful, like really mesmerizing digital art. I had never heard of a Mandelbrot before reading your blog post the other day. Love the idea of Mandelbrot March or May. That should be fun. I look forward to seeing and learning more!
By Katherine Wikoff on November 18, 2025 at 5:47 am
Heh, yeah, I can see a belt with that horizontal pattern. There are many such spots in the Mandelbrot, so one could produce a whole line of “Mandelbelts”. 😊
I’m pretty sure I won’t get to that post series until next year (which isn’t all that far away, come to think of it), but in the meantime, here are two links to older posts that get into how the Mandelbrot works.
The Mighty Mandelbrot is the first time I discussed it in any detail.
Mandelbrot Reality gets more into some specifics of how the set is calculated.
By Wyrd Smythe on November 18, 2025 at 9:29 am
“The Mighty Mandelbrot”—what a great title!
By Katherine Wikoff on November 18, 2025 at 1:10 pm
[…] Last post I wrote, “For two weeks I’ve indulged in intense 12+ hour days on a self-education project in Python and its Tk module.” And it was intense; I’ve spent all week recovering. […]
By Friday Notes (Nov 21, 2025) | Logos con carne on November 21, 2025 at 9:15 am
[…] A few posts ago I wrote that for “two weeks I’ve indulged in intense 12+ hour days on a self-education project in Python and its Tk module.” The end result of the binge is seven new apps (so far; more to come) and a good starting grasp of how to make some fairly decent windowing apps in Microsoft Windows. […]
By November Coding Binge | Logos con carne on November 27, 2025 at 1:11 pm