Another Mandelbrot Monday

Time for another Mandelbrot Monday. I’ve mentioned before that aimlessly playing around with Mandelbrot zooms gets old fairly quickly. I find that I do it for a little while, lose interest for a long while, and then pick it up again for a little while.

I’m in the lost interest phase right now — have been for a couple of months. I think I’ll cool my jets until May, when I’m planning a series of posts (“Mandelbrot May”) exploring the Mandelbrot set and how images of it are made.

But I still have images from previous phases to share, so off we go…

For a brief refresher on the Mandelbrot set, see the beginning of the first post in the Mandelbrot Monday series. See the beginning of the second post for a few more details.

The TL;DR is that the Mandelbrot is a set of simply connected points on the complex plane. All points are found between -2.0 and +0.5 in the X coordinate (the horizontal real axis) and between -1.25 and +1.25 in the Y coordinate (the vertical “imaginary” axis):

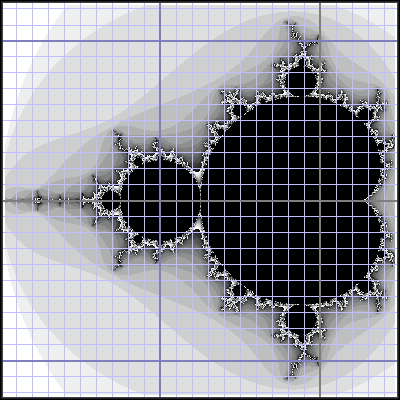
In most renderings, the points inside the set are colored black and points outside the set are colored something other than black (shades of gray in the image above but typically a palette of colors).

The Mandelbrot is most interesting at the border between the inside and outside of the set. This border cannot be fully computed (because of the Turing Halting problem), it can only be computed to some resolution. That’s sort of what Mandelbrot zooms are — magnifying some tiny portion of the border region to increasing, but never ending, levels of detail.

And, of course, a nice palette. The colors essentially encode distance from the Mandelbrot — in the image above, the gray shade gets lighter the further it is from the black region. Usually, though, we use something more colorful:

x: -1.2625192184948280184105536769504
y: +0.40841294722155143269694497619992
magnification: 1.2967064e22

All the structure in these comes from the chaotic twisting and winding of the Mandelbrot set. (“Infinite Diversity in Infinite Combination”) Each image demonstrates mathematical chaos. The image varies considerably from pixel to adjacent pixel, yet each pixel represents a tiny variation in input. For the image above, along the X-axis (horizontally), the variation is:

left:  -1.2625192184948280184107593261758
right: -1.262519218494828018410348027725
diff:   0.0000000000000000000004112984508

Along the Y-axis (vertical), the variation is:

top: +0.40841294722155143269706065388918
bot: +0.40841294722155143269682929851066
diff: 0.00000000000000000000023135537852

That’s all the variation there is across the whole image (and this one is zoomed down to only 10²² — the variation is considerably less in deeper zooms.

Therefore, because these images are 3840 pixels × 2160 pixels, the variation from pixel to pixel is:

0.00000000000000000000000010710897

In both the horizontal and vertical directions. This tiny variation in the input causes each pixel to differ — chaos visualized.

x: +0.2330064105101592216
y: +0.5503121225675308081
magnification: 3.4163793e9

A fairly shallow zoom, only 10⁹, but in a striking place along the Mandelbrot border: the butt crack (left center in the first image above). That accounts for the swirly feathery shapes in this image.

This is the only image today with a prominent mini-Mandelbrot, though every image has an infinite number of them lurking at deeper zoom levels, and a few below have a smaller mini.

x: -0.8563480627613242939405832313504679977577752236105
y: -0.242879160570708989459793424000944533721700612189
magnification: 9.1655441e38

This is one of my favorites. I like the monochromatic surrounding with the islands of bright color. And I like the feathery shapes with lots of little “question marks” and branches.

Note, as always, the rotational symmetry. Some images also have horizontal and/or vertical symmetry (like the first one presented above, which has both). The Mandelbrot set itself has vertical symmetry. The part below the X-axis is a mirror reflection of the part above (or vice-versa).

x: -0.64188589656354808793146967261
y: +0.0000000860930859117602508121328612544
magnification: 3.8137627e20

Bit of a different look because we’re in the “needle” region — the spike that sticks out to the left of the main cardioid shape. Zooms in this region have a characteristic spikiness. The plant-like branching secondary pattern comes from having zoomed past a larger mini-brot in a region with such branching and then zooming into the needle region of a deeper mini-brot.

Be sure to look at this one full size so you can see all the tiny points of light in the outer surround. And note the leaf-like patterns they make.

x: -0.8610345962019803033253892955122786587060386081...
y: +0.2155477088976018650367076164889874233958733072...
magnification: 3.0151543e45

My gold/bronze palette. This one feels dynamic, like it’s spinning. I like the streamer pairs extending from the “spinning wheel”. There’s a second set inside, spiraling up from the little mini-brot to the fat black circle. Then a bunch of jagged “spokes” joining to the outer wheel.

Fairly deep zoom, too. (Well, not really in the general scope of Mandelbrot zooms. Serious zooms can go far beyond 10¹⁰⁰⁰, and some go beyond 10¹⁰⁰⁰⁰ — which takes some time to render. Like days on most equipment.)

x: -1.98546779459892185386511035254331597085652841989...
y: -0.00001221361960184800891136496504986581349564293...
magnification: 8.4320307e52

Mmmm, minty! Looks edible. I’m not usually a fan of green palettes, but sometimes they work for me. The amount of swirl depends on where along the border the zoom is. Swirls lurk in the cracks and clefts (such as in the “butt crack” but also in the clefts between the larger circular bays and the main cardioid.

This one is the deepest zoom today — 10⁵² (but still quite shallow in the general scheme of such things).

x: -1.0280346788
y: +0.36113315573
magnification: 280.70247

This is a very shallow zoom on one of the tendrils that sticks up from the largest circular bay directly to the left of the main cardioid. As the coordinates indicate, very near x=-1.

But it’s one of my favorite images because it uses a slightly different coloring algorithm, one called Circular Orbit traps. That’s what creates those ghostly sphere shapes hovering in the background. I really like the combination of those ghost spheres and the lightning-strike coloring of the tendril.

x: -0.71004168188148347443119195447617455065195
y: 0.3130997443989112676599669230902931796029
magnification: 2.8248447e29

As always, it’s the fine detail that makes the image interesting, but I really like this purple-blue-white palette, too. Another color combo that looks somehow like tasty candy.

This, and the bronze/gold one above, illustrate something we see a lot while zooming down towards a mini-brot. There is a “radial frequency” — the number of branches coming from a central point. In the image above, 16 branches extending from the large cyan circle, but the circle itself is made from a much larger number of branches coming from the 16 “nodes” inside the circle.

Those join down to 16 slightly smaller nodes, but those nodes have even smaller nodes between them, so the radial frequency jumps from 16 to 32. They extend from the smaller inner ring that again has a very high radial frequency.

Briefly, inside that second ring, we’re down to a radial frequency of 8, but it quickly becomes 16 and then more.

The point being the radial frequency changes constantly during a zoom with a tendency to become very high as you approach a mini-brot. The minimum is two, and it changes by powers of two (2, 4, 8, 16, 32, 64, and so on).

x: -0.70694142421087406956502426699410755295
y: +0.24903650193950589798887699769768338535
magnification: 7.4147365e27
angle: -42.841

A striking pattern that comes from zooming in near the outside end of the smaller circular bays that line the main cardioid.

Each circular bay has a “stalk” extending away from the Mandelbrot, and images like the above are zooms of parts of the stalk. These have interesting nodes with high radial frequencies — lots of branches extending from the nodes.

x: -0.706941424210874069565024266993500203725512225
y: +0.249036501939505897988876997696346902854007255
magnification: 2.4203426e34
angle: -42.841

This is a deeper zoom in the same location as the previous one. In this one, the cyan part of the color palette is more prominent than the navy blue in the first one.

And we found the little mini-brot at the end of the zoom. Note again the nodes with lots of branches.

x: -0.09046968813930150643763
y: +0.6495181924371888788288
magnification: 9.1508425E12

A fairly shallow zoom but in a region where the chaos is strong. I like the feathery patterns we get in this region. Notice how the large fans have small curlicue shapes that approach them. The Mandelbrot is self-similar in contrast to fractals that are self-identical as all scales. As you zoom in, the patterns are similar but not identical.

Trying something a bit different with the color palette. Tans and faded greens.

x: -0.09046968813928845855584443
y: +0.64951819243718293162493285
magnification: 1.050956e16

Same location as above but diving a bit deeper. Same palette but falling in a dark and murky part of it.

I do like the pattern, but I’m not thrilled with the palette.

x: -0.09046968813928853425976987528604849905
y: +0.6495181924371829612257174941190991475
magnification: 1.6115995e27

Still in the same location but now zoomed to 10²⁷ where the chaos is strong.

I changed the palette on this one because I was trying to make some Valentine’s Day Mandelbrot zooms for my Fractal Fridays on Substack (where I post two or three images as Substack Notes most Fridays).

I made these last October… and forgot to post them on the only day that would have made sense: this past Friday, February 13th.

On the other hand:

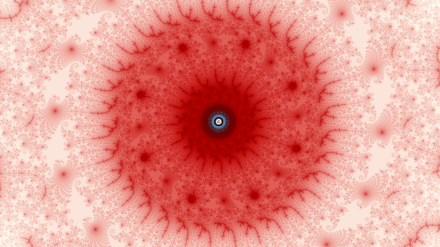
x: -0.0904696881392885342597698752838501769369
y: +0.649518192437182961225717494170401848592
magnification: 1.5579199e29

I wasn’t that happy with this, what I intended for the key Valentine’s Day Mandelbrot zoom. Same location as the three above, but with a mostly red palette.

But meh. I’m not into Valentine’s Day, anyway. Never was. I don’t like (nor need) being told to be romantic. Same with Mother’s Day and Father’s Day. Don’t care to join the crowd forced to stand up on command and pledge allegiance to parents or mate. I’ve just never been down with pro forma.

§ §

Stay chaotic, my friends! Go forth and spread beauty and light.

∇